当前位置：首页 > ai >正文

数学证明 | 逻辑的力量

ai 2025/5/11 6:31:54

注：本文为“数学证明”相关文章合辑。

略作重排，未整理去重。
如有内容异常，请看原文。

数学证明到底是什么？丨展卷

原创 William Dunham
返朴
2022 年 06 月 19 日 08:00 湖南

数学史家，穆伦堡学院名誉 Truman Koehler 数学教授威廉・邓纳姆于 1994 年出版 The Mathematical Universe 一书，以 26 个英文字母作为标题讲述数学史上重要的问题和人物。本文选自 J——Justification，论证。数学与其他学科最大的不同就在于，命题需要证明。数千年来，数学正因为此发展进步，人类一步步攀上智慧的高峰。而且，在作者看来，“数学证明的标准不同于其他任何人类活动领域中的标准。”那么，数学定理的证明到底是什么呢？本文给出了四个基本原则，阐述涉及数学证明本质的非常有意义的问题。

本文经授权选自《数学那些事：伟大的问题与非凡的人》（图灵｜人民邮电出版，2022.3），标题为编者所加。

撰文丨威廉・邓纳姆（William Dunham，美国穆伦堡学院数学教授）
翻译丨冯速

“证明，”数学家迈克尔・阿蒂亚（Michael Atiyah，1929-2019）曾说，“它是胶水，把数学粘到了一起。”显然，这一观点想说的是，证明或者说论证是数学的化身。

这样的观点可能会引起争议。数学这个学科涉及的范围如此广泛，它可以包含各种活动，如估值、构造反例、测试特殊案例以及解决日常问题等。数学家也不必每天 24 小时都在证明定理。

然而，即便理论命题的逻辑论证不是数学的全部活动，它也肯定是这个学科的特征。数学离不开其他各个方面的学术努力，就像它离不开证明、推理以及逻辑演绎一样。在比较数学与逻辑的关系时，伯特兰・罗素断言：“已经无法在二者之间划出界线了；事实上，二者是一体的。”

本书已经分析了很多数学论证。在第 A 章（Arithmetic 算术）中，我们证明了质数的无穷性；在第 H 章中，我们证明了毕达哥拉斯定理。就一般数学论证而言，这些证明相当简单。其他论证却需要很多页、很多章节，甚至很多卷才能得出它们的最终结论。相应的智力要求不见得适合每一个人，正如谦逊的查尔斯・达尔文表明的那样：“我跟随漫长而纯粹抽象的思维轨迹的能力极其有限，因此我从来不可能在形而上学或者数学上取得成功。”或者，用约翰・洛克（John Locke）更简短的话说：“数学证明像钻石一样既坚硬又清透。”

数学定理的证明到底是什么呢？这个问题并不像它看起来那样一目了然，因为它涉及哲学、心理学和数学各方面的因素。亚里士多德对此有深刻的理解，他把证明描述为 “不是表面上的陈述而是内心的冥想。”

罗素也做出了令人信服的评论：数学家永远不可能把 “完整的推理过程” 写到纸上，而一定会放置 “足以使训练有素的大脑信服的证明摘要”。他想要说的就是，任何数学陈述都是建立在另一些陈述和定义的基础之上的，这些陈述和定义又是建立在更多的陈述和定义的基础之上的，因此要求证明沿着每一个逻辑步骤追踪回来，也许有点鲁莽。然而在 20 世纪初，当罗素与艾尔弗雷德・诺思・怀特海（Alfred North Whitehead，1861-1947）一起合著巨著《数学原理》时，他似乎忘记了自己给世人的忠告。在这本著作中，他们尝试着把整个数学回推到基础的逻辑原理，并在这一过程中保留了细节。其结果是非常折磨人的。他们的展开如此周密，在他们最终证明了 $1 + 1 = 2$ 之前，此书已达 362 页，这一证明在 “基数算术导言” 一章的 54.43 节（参见图 1）。《数学原理》使论证变得疯狂。

图 1 罗素和怀特海证明 $1 + 1 = 2$ 丨摘自艾尔弗雷德・诺思・怀特海和伯特兰・罗素于 1910 年合写的《数学原理》的第 1 卷。剑桥大学出版社惠允

在本章，我们要试着保持头脑清醒。按照我们的意思，证明就是在逻辑法则的范围内精心制作的推理，对于一个论断的正确性，它无懈可击，令人信服。像 “说服谁？” 或者 “按照谁的标准无懈可击？” 等一类问题留作以后再议。

当然，我们也可以选择考虑什么不是证明。借助直观、常识，或者更糟，借助暗示的陈述都不是论证。刑事诉讼中作为有罪证明的 “排除一切怀疑” 的证明，也不是我们所说的论证。数学家认为，证明不仅能排除合理的疑问，而且能够排除所有疑问。

我们可以从许多不同的方向展开关于数学论证的讨论。这里，我们给出四个重要的基本原则，并逐个阐述涉及数学证明本质的非常有意义的问题。

基本原则 1：个案不充分

无论在科学中，还是在日常生活中，当实验反复肯定某个原则之后，我们就倾向于接受它的真实性。如果肯定的案例数量足够大，我们就说有了一个 “被证实的法则”。

但是，对于数学家来说，几个案例的结果尽管可能给出一些提示，但绝不是证明。下面给出这种现象的一个例子，考虑

猜想把一个正整数代入多项式 $f(n)=n^7-28n^6+322n^5-1960n^4+6769n^3-13132n^2+13069n-5040$ ，我们总可以得到原来的正整数。用符号表示就是断言：对于任意正整数 $n$ 都有 $f (n) = n$ 。

这是真的吗？显然，我们可以代入几个正整数看一看有什么结果。当 $n = 1$ 时，我们得到

$\begin{align*} f(1)&=1-28+322-1960+6769-13132+13069-5040\\ &=1， \end{align*}$

显然断言成立。如果我们代入 $n = 2$ ，计算结果为

$\begin{align*} f(2)&=2^7-28\times2^6+322\times2^5-1960\times2^4+6769\times2^3-13132\times2^2+13069\times2-5040 \\ &=2 \end{align*}$

这一次断言仍然成立。我们希望读者拿出计算器，验证一下 $f (3) = 3$ ， $f (4) = 4$ ， $f (5) = 5$ ， $f (6) = 6$ ，甚至 $f (7) = 7$ 。

这个论断的证据似乎建立起来了。有些人，特别是那些对这样机械式的计算没有热情的人也许已经宣布这个陈述是真的。但是，它不是真的。代入 $n = 8$ 时，我们得到

$\begin{align*} f(8)&= {{8}^{7}}-28\times {{8}^{6}}+322\times {{8}^{5}}-1960\times {{8}^{4}}+6769\times {{8}^{3}}-13132\times {{8}^{2}}+13069\times 8-5040 \\ &= 5048 \end{align*}$

结果不是我们期望的 8。进一步的计算表明 $f (9) = 40329$ ， $f (10) = 181450$ ， $f (11) = 640811$ ，所以此断言不仅失败了，而且错得惊人。对于由 $n = 1, 2, 3, 4, 5, 6, 7$ 时都为真得出 $n$ 为任意正整数时都为真的猜测实际上是不正确的。

我们把下面这个表达式展开并合并同类项，就可以得到刚才讨论的多项式

$f (n) = n + [(n - 1) (n - 2) (n - 3) (n - 4) (n - 5) (n - 6) (n - 7)]$

显然，对于 $n = 1$ ，项 $(n - 1)$ 为零，因此方括号中的所有乘积都为零；因此 $f (1) = 1 + 0 = 1$ 。如果 $n = 2$ ，那么 $n - 2 = 0$ ，所以 $f (2) = 2 + 0 = 2$ 。类似地， $f (3) = 3 + 0 = 3$ ，一直到 $f (7) = 7 + 0 = 7$ 。但是这之后括号里的项不再是零，例如 $f (8) = 8 + 7! = 5048$ 。

这引出下面这样一个富有挑战性的扩展命题。假设我们引入

$g(n)=n+[(n-1)(n-2)(n-3)\dots(n-1000000)]$

并猜测对于所有正整数 $n$ ，有 $g (n) = n$ 。

我们做乘法且合并 $g (n)$ 的项，就得到一个一百万次的惊人方程。通过与上面完全相同的推理，我们将发现 $g (1) = 1$ ， $g (2) = 2$ ，一直到 $g (1000000) = 1000000$ 。

在发现了一百万个连续正确的证据之后，任何思维正常的人都会怀疑 $g (n)$ 是否总是产生 $n$ 。对于任何人——除了数学家之外，一百万次连续成功都等同于排除了所有值得怀疑的证明。然而，再接下来验证一下， $g (1000001)$ 实际上等于 $1000001 + 1000000!$ ，这个数非常大，显然超过 1000001。

上面这个例子强调了关于数学证明的第一个基本原则：我们必须对所有可能的情况进行证明，而不仅是对几百万个情况进行证明。

基本原则 2：越简单越好

数学家赞美那些巧妙的证明。但是，数学家更赞美那些既巧妙又经济的证明，即那些直击要害、直达目标的没有多余之处的简洁推理。这样的证明被认为是优雅的。

数学的优雅与其他创意作品的优雅没有什么不同。它与莫奈的油画艺术的优雅有很多共同之处，仅用寥寥几笔勾勒或几行诗描绘的法国乡村风景，胜过长篇大论。优雅在本质上属于美学范畴，而不是数学的特性。

同任何理想一样，优雅不是总能够实现的。数学家们为简短、清晰明了的证明而奋斗，但是经常必须忍受令人讨厌的烦琐事物。例如，抽象代数中有限单群分类的证明用了 5000 多页纸（最终检验通过时）。寻求优雅的人请另寻出路。

相比之下，数学家达到的终极优雅是所谓的 “无言的证明”，在这样的证明中一个极好的令人信服的图示就传达了证明，甚至不需要任何解释。很难比它更优雅了。例如，考虑下面的例子。

定理如果 $n$ 是正整数，那么 g
$\sum_{k=1}^{n} k = \frac{n(n+1)}{2}$
这个定理说的是，当我们把前 $n$ 个正整数相加时，和总是 $n$ 与 $n + 1$ 的积的一半。我们可以用几个特殊的数验证一下，例如， $n = 6$ ，

$1+2+3+4+5+6=21=\frac{1}{2}6\left( 6+1 \right)$

但是第一个基本原则警告说，只有傻子才会依据一个案例就匆匆得出结论。我们要利用图 2 去证明这个命题。

图 2

这里我们采用由一块加上两块再加上三块等这样阶梯式的结构，如图 2 阴影部分所示；用方块摆出 $n\times(n+1)$ 的矩形排列。这个矩形是由两个完全相图同的阶梯组成的，矩形的面积等于它的长和宽的积，即 $n\times(n+1)$ ，因此这个阶梯的面积一定是矩形面积的一半，即

$1+2+3+…+n=\sum_{k=1}^{n} k = \frac{n(n+1)}{2}$

证毕。

读者也许观察到这个 “无言的证明” 仍然伴随着一段文字解释。但是，语言的解释的确没有必要，这个图示值千言万语。（“无言的证明” 是美国《大学数学杂志》的固定专栏。）

下面是另一个不可否认的优雅证明。假设我们从 1 开始把正奇数依次相加：

$1+3+5+7+9+11+13+\dots$

一些经验提示我们，无论把这个加法进行到什么时候，其结果总是完全平方数。例如，

$1+3+5=9=3^2$
$1+3+5+7+9=25=5^2$
$1+3+5+7+9+11+13+15+17+19+21+23+25+27=196=14^2$

这永远为真吗？如果是，我们如何证明这个一般结果？

下面的推理需要一点代数知识，根据观察：偶数是 2 的倍数，因此对某个整数 $n$ ，其形式是 $2 n$ ；而奇数比 2 的倍数少 1，因此对某个整数 $n$ ，其形式是 $2 n - 1$ 。

定理从 1 开始的连续奇数之和是一个完全平方。

证明设 $S$ 是从 1 开始到 $2 n - 1$ ( $n > 0$ ) 的连续奇数之和，即

$S=1+3+5+7+\dots+(2n-1)$

显然我们可以求从 1 到 $2 n$ 为止的所有整数的和，然后再减去偶数之和就可以得到连续奇数之和。换句话说

$\begin{align*} S & =[1+2+3+4+5+\ldots +(2n-1)+2n]-(2+4+6+8+\ldots +2n) \\ & =[1+2+3+4+5+\ldots +(2n-1)+2n]-2(1+2+3+4+\ldots +n) \end{align*}$

这里，我们从第二个方括号的表达式中提出了一个因子 2。

第一个方括号中是从 1 到 $2 n$ 的所有整数的和，而第二个方括号中是从 1 到 $n$ 的所有整数的和。图 2 的 “无言的证明” 展示了如何求这样的整数和，所以我们两次利用那个结果：

$\sum_{k=1}^{n} k = \frac{n(n+1)}{2}$

化简上式得到

$\frac{2n(2n+1)}{2} - 2 \times \frac{n(n+1)}{2} = n^2$

因此无论 $n$ 是什么值，连续奇数之和都是一个完全平方 $n^2$ 。证明完毕。

一句话，这个证明是优雅的。但是，如果它是我们寻找的那种优雅，那么图 3 则给出了另一个更短的证明，一个无言的证明。这里奇数是一个方块、三个方块、五个方块，以此类推，按特殊方法排列。我们从左下角的一个方块开始，三个有阴影的方块包围着它形成一个 $2\times2$ 的正方形，五个没阴影的方块包围着前面这些方块形成一个 $3\times3$ 的正方形，接下来就是七个有阴影的方块包围着前面这些方块形成一个 $4\times4$ 的正方形，以此类推。这张图示清楚地表明从 1 开始的连续奇数的和总是产生一个（几何的）平方。这个证明非常自然。早在 2000 年前古希腊人就知道它了，现代的后辈可以通过构建方块模仿这一证明。

图 3

温斯顿・丘吉尔（Winston Churchill）说：“短小的词为佳，而既古老又短小的词为最佳。” 我们可以重新描述这个优雅推理：古老的证明为佳，而既古老又短小的证明为最佳。

基本原则 3：反例的价值

数学中有一个非常严酷的现实：为了证明一个一般的陈述需要一个一般的推理；但为了反驳它，只需要一个特殊的例子，一个使这个陈述失败的例子。后者称为反例，一个好的反例价值如金。例如，假设我们有下面的猜测。

猜测如果 $a$ 和 $b$ 是正整数，则
$\sqrt{a^2 + b^2} = a + b$

年复一年，数以万计的学生曾经使用过这个特殊的公式，这可以从任何一名数学老师那里得到证实。但是这个公式是不成立的，为了说明这一点，我们需要一个反例。如果 $a = 3$ ， $b = 4$ ，那么
$\sqrt{3^2 + 4^2} = 5$
而 $a + b = 3 + 4 = 7$ 。仅这一个反例就足以把这个猜测送进数学的垃圾堆。

我们强调，尽管可能需要 50 页纸的推理来证明一个定理，但是只要一行反例就可以反驳它。在证明和反证之间的大战中，似乎没有一个公平的竞争环境。但是，还是要说一句警告的话：寻找反例不像看起来那样容易。下面的故事就是一个例子。

两个多世纪前，欧拉猜测至少要把三个完全立方加起来才能得到另一个完全立方，至少要把四个完全四次幂相加才能得到另一个完全四次幂，至少要把五个完全五次幂相加才能得到另一个完全五次幂，等等。

作为一个例子，我们把这些完全立方相加： $3^3+4^3+5^3=27+64+125$ ，得到和 216，它正好是 $6^3$ 。这里，三个立方合并起来得到了一个立方，但是欧拉断定并证明了两个立方之和永远不会得到一个完全立方。

读过第 F 章的读者应该意识到，这是费马最后定理的特殊情况 ( $n = 3$ )。

提高次数，我们能够找到四个完全四次幂，它们之和等于一个四次幂。例如，考虑下面绝非一目了然的例子：

$30^4+120^4+272^4+315^4=353^4$

欧拉猜测三个四次幂之和不会产生另一个四次幂，但是没有给出证明。一般地，他说至少需要 $n$ 个 $n$ 次幂，使得它们之和等于另一个 $n$ 次幂。

这件事在 1778 年成立，近两个世纪后它仍然成立。信任欧拉的人不能用证明来肯定欧拉的猜测，但不相信欧拉的人也不能构造出一个特殊的反例来驳倒它。这个问题是一个未解问题。

到了 1966 年，数学家利昂・兰德（Leon Lander）和托马斯・帕金（Thomas Parkin）发现了下面这个例子：

$27^5+84^5+110^5+133^5=144^5$

四个五次幂却产生另外一个五次幂。欧拉被驳倒了。而二十年后强大的计算机炫耀了一下它的电子大脑的威力，用了上百小时找到了下面这个非常有力的反例：

$95800^4+217519^4+414560^4=422481^4$

这表明三个四次幂，而不是欧拉说的四个四次幂，也能生成一个四次幂。

寻找这些反例需要大量努力，甚至动用了计算机的力量，这是非常惊人的。这显然给出了基本原则 #3 的一个推论：有时候反证比证明更难。

基本原则 4：可以证明否定

在理发店或快餐店里，我们经常听到这样一句老话：你不能证明否定。它可能是由下面这样的对话引发的：

A：“超市小报说一个小妖精中了奖。”
B：“没有小妖精这种东西。”
A：“你说什么呢？”
B：“我说小妖精不存在。”
A：“你肯定吗？你能够证明它不存在吗？”
B：“当然…… 不能。但是你也不能证明它存在。”

这个对话很长。用一句话说，它声称我们绝对不能证明小妖精不存在。

数学家知道得更清楚。一些最伟大、最重要的数学推理所论证的就是某些数、某些形状、某些几何结构不存在且不可能存在。人们使用最猛烈的武器，即理性的、严密的逻辑确立了这些不存在的事物。

认为否定不可证明的这种普遍观念本质上是错误的。为了证明小妖精不存在，我们似乎需要翻遍爱尔兰岛上的每一块石头，翻遍南极洲的每一座冰山。当然这是不可能实现的野心。

为了在逻辑上确立不存在的事物，数学家采用了一种非常不同然而又非常完美的策略：假设这个对象的确存在，然后再追踪由此产生的结果。如果我们能够证明存在的假设将导致一个矛盾的话，那么逻辑法则允许我们得出结论：我们在第一步中所做的存在的假设是错误的。因此，我们就能够得出这个事物不存在的毫无争议的结论，同时也说明一个事实，即我们采用了一个非直接的途径所得到的这个结果是正确的。

在第 Q 章中，我们将讨论最著名的不存在证明：为什么不存在等于 $\sqrt{2}$ 的分数？然而，对于我们眼前的目标，下面这个例子就足够了。

定理不存在边长分别为 2, 3, 4, 10 的四边形。

处理这个问题的一个实用方法是截出这些长度的木棍，然后试着把它们摆放成一个有四条边的图形。这只是一个说明，然而在逻辑的意义下，这相当于要在某块岩石下找到一个小妖精。即使我们花费了好多年都没有成功地用这四根木棍摆出一个四边形，也不能排除也许某个人在某天成功地把它们摆成四边形的可能性。

合理的方法是我们要间接地证明一个否定。开始我们假设存在一个四边形，它的边长分别是 2, 3, 4, 10，然后再设法生成一个矛盾，这是一个战略上的飞跃。

我们假设的四边形如图 4 所示。画出虚线所示的对角线，它把这个四边形分成两个三角形，并设 $x$ 是这条对角线的长度。第 G 章（古希腊几何）已经说明过，欧几里得证明了三角形的任意一条边小于其他两条边的和。因此在 $\triangle ABC$ 中，我们知道 $10 < 4 + x$ 。同样在 $\triangle ADC$ 中，有 $x < 2 + 3$ 。把这两个不等式结合起来得到

$10 < 4 + x < 4 + (2 + 3) = 9$

根据上面的不等式，得到 $10 < 9$ 。这是不可能的。我们最初所做的存在这种特殊的四边形的假设导出了这一矛盾，所以说我们的假设是无效的。

图 4 和图 5

这个四边形的四条边长的出现顺序（按顺时针）是 10, 2, 3, 4。还有其他方法放置这四条边，如图 5 所示，同样的推理也导出一个矛盾。此时是 $10 < 2 + x < 2 + (3 + 4) = 9$ 。这是不可能的。

没有必要再继续寻找了，重新布局再多次也是没有意义的。这样的四边形是不可能存在的。我们最终证明了一个否定。

基于矛盾的证明是一个非常好的逻辑策略。假设我们想要证明的反面是成立的，我们似乎是在毁灭自己的目标。但是，最后我们避开了灾难。哈代把基于矛盾的证明描述为 “数学家最好的武器之一。它远比其他任何先手棋策略好得多：象棋手也许要牺牲一个小卒或者其他一枚棋子，但是数学家牺牲的却是 整盘游戏”。

问题：还需要人类吗？

大约在 20 世纪 70 年代到 80 年代期间，有一种令人不安的映像闯入数学家的意识之中。这就是计算机映像，它以光一样的速度和实质上的可靠性接手了证明定理的工作。

我们已经提到了几个例子，在这些例子中，计算机提供了证否某个陈述的反例。 $95800^4+217519^4+414560^4=422481^4$ 的发现给予欧拉的猜测致命的一击，很难想象人类要花费多长时间去寻找这样一个反例。这是完全适合计算机的问题。

令整个数学界感到困惑的是此后出现的一些利用计算机来证明定理的情况。这些情况往往把一个定理分解成很多子情况，假如肯定了每一种子情况，那么就可以断定解决了整个问题。遗憾的是，这种分析通常需要考虑上百种情况，需要成千上万次计算，而人类没有可能重复所有步骤。总之，这样的证明只能通过其他机器来检查。

1976 年，计算机证明凭借解决四色猜想问题戏剧般地登上了数学舞台。所谓的四色猜想，是任何画在平面的地图都可以用四种（或少于四种）颜色着色，使得拥有共同边界的任意两个区域都被涂上不同的颜色。（例如在图 6 中，我们不想给区域 A 和 B 都涂上红色，因为那样一来它们的公共边界线会被遮住。我们允许给相交于一点的两个区域，如区域 A 和 C 涂上相同的颜色，当然一个点不是边界线。）

图 6 和图 7

四色猜想诞生于 1852 年，在接下来的一个世纪里引起了广泛的关注。有几个问题很快就被解决了，比如任何平面地图肯定可以用五种颜色着色，还有就是用三种颜色着色地图是不充分的。图 7 就给出了这样的一个地图。在这张图上，我们必须使区域 A、B 和 C 有不同的颜色，因为它们每对都有共同的边界，但是接下来，除非使用第四种颜色，否则不可能给区域 D 着色。

因此，五种颜色（可能）太多而三种颜色又不够。显然这就需要四种颜色。四种颜色足以给任何平面地图着色吗？

我们之前的讨论表明，要想解决这个问题只有两种选择：要么提出一个特殊的反例，即给出一种不能用四种颜色着色的特殊地图；要么设计一个一般的证明，证明任何地图都能够这样着色。对于数学家来说，这个反例很难找到。他们制作的每一张地图无论多么错综复杂，都能仅用红色、黄色、蓝色和绿色着色。（有蜡笔的读者也许想立即勾画出一张地图，然后尝试一下。）

但是，正如我们反复提醒的那样，证明可不光是找到几个反例就算完成了。以前人们会发疯地寻找一般推理，但事实证明每一种情况都与寻找反例一样困难。局势处于停顿的状态。

后来，美国伊利诺伊大学的阿佩尔（Kenneth Appel）与哈肯（Wolfgang Haken）宣布四色猜想为真，震撼了整个数学界。令人们感到震惊的不是这个结论，而是他们的证明技术：计算机完成了证明中最艰难的部分。

阿佩尔和哈肯处理这个问题的方法是，把所有平面地图分成某些类型，然后分别分析每一种类型。遗憾的是，一共有上百种类型需要检查，每一种类型都给高速计算机带来大量的工作。最后，计算机宣告这个猜测是真的，即所有可能的类型都可以用四种颜色着色。这个定理得到了证明。

这是真的吗？说句公道话，当时一种不安的情绪在整个数学界蔓延。这算得上是一个正确的论证吗？令人困惑的是，回答这个问题需要一个真正的有血有肉的人每周工作 60 小时，花费大约 100 000 年的时间去检查计算机的计算。甚至是最健康、最乐观的人也不可能活那么长时间，总之，谁愿意花这个工夫呢？

如果程序出现了错误怎么办？如果功率突增使得计算机跳过关键的步骤怎么办？如果计算机的硬件设计暴露出极少见的微小缺陷怎么办？总之，我们能够相信机器大脑能给我们真理吗？正如数学家罗恩・格雷厄姆（Ron Graham）在考虑这些复杂问题时提出的那样：“实质的问题是这样的：如果没有人能够检查一个证明，它还是一个真正的证明吗？”

直到今天，这个问题也没有明确的答案，尽管随着计算机证明变得更加普遍，也许数学家们对它们的出现会感到稍舒服些，但是，公正地说，如果四色定理拥有写了两页纸那样短小、睿智而优雅的证明，而不是依靠计算机的蛮力得到的证明，那么大多数数学家也许会轻松地喘口气。传统主义者希望古老的数学不要被接上电源。

“还需要人类吗？” 此时这个问题的答案仍然是 “需要”。毕竟得有人打开空调吧。但是我们得承认这个观点也许是有偏见的，因为它的支持者本身是人。

我们关于数学论证的讨论到此就结束了。显然，还有很多话要说，也应该引出其他的议题，应该提出其他的基本原则。但是，我们最终得出的最重要的结论是：无论是优雅还是麻烦，是直接还是间接，是依赖于计算机还是人力，数学证明的标准不同于其他任何人类活动领域中的标准。

我们为什么需要证明？揭秘数学证明的迷人世界

原创 Freiberger
科学演绎法
2024 年 04 月 24 日 20:15 河南

【科学演绎法】编辑：

数学是我们探索理解宇宙和追求真理的基石灯。在本文中，我们把目光聚集到数学证明的奥妙和美丽上。证明，一个古老却强大的工具，通过证明，数学家们可以确立一个定理的正确性，使其成为被全人类接受的事实。

亲爱的读者，让我们一同进入数学证明的奇妙世界，揭示隐藏在几何图形、符号序列和逻辑关联背后的秘密。就像是探索一个未知的森林，我们将逐步深入理解数学逻辑的力量，从最基本的归纳、演绎推理，到深奥的公理系统。

追随欧几里得的脚步，我们将看到，从几个直观简单的公理出发，如何构建出一个的欧氏几何世界模型。《几何原本》不仅奠定了几何学的基础，也展示了严谨推理的力量。这些基本公理如何启发我们对整个数学体系进行深刻的思考？而最后一条公理，它如何又发展成为理解宇宙的钥匙？

它挑战数学家的思维，引领人们思索一个问题：在不同的世界里，数学真理是否依然能保持其永恒的光芒？

我们也将深入探讨计算机在数学证明中的角色。在过去的几十年中，计算机已然成为数学家们不可或缺的助手，但是，它们会不会从辅助工具变为主导者？在这个 AI 技术层出不穷的时代，这个问题变得愈发迫切。

下面开始阅读，启动我们的数学探索之旅。

作者 | Marianne Freiberger
译者 | 小白

证明是一种逻辑论证，它可以毫无疑问地确定某件事或某句话是真实成立的。数学家是如何着手证明自己的论点的呢？他们又是为什么如此热衷于证明呢？

▲ 几何原本中有许多证明的技巧，上图是俄克喜林库斯 29 号莎草纸《几何原本》卷 2 关于命题 5 的证明

证明的方式有什么？

在日常生活中，当我们使用理性分析时，我们通常会使用两种形式的推理：归纳推理和演绎推理。

归纳推理 (Inductive Reasoning) 会利用我们看到过的东西中归纳出一个一般性的结论。

例如，如果你见过的所有羊都是白色的，就可能会得出结论，说所有的羊都是白色的。

这种形式的推理非常有用，科学家们以类似的方式，根据他们所做的观察来形成他们的理论。

但这种推理并非无懈可击的，因为能否肯定见过宇宙中的每一只羊了吗？所以永远不能确定有没有一只黑色的羊藏在某个尚未看到的地方，所以不能确定这个结论是绝对真理。

比如，再来看数学中的一个有意思的例子：

或许根据上面这些示例，能否宣称找到了某种模式，归纳出了这积分的公式了吗？先等一等，再往后算两个看看：

积分的结果已经发生了变化，所以这样在使用归纳推理，新的证据出现时，就必须修改结论。

另一种推理被称为 演绎推理 (Deductive Reasoning)，它与归纳推理的证明手法截然不同。从一个正确的概括性陈述开始，然后对一个具体的案例得出结论。

例如，你知道这样事实，所有的羊都喜欢吃草，并且知道站在面前的就是一只羊，那么你肯定也知道这只也喜欢吃草。

这种形式的推理是无懈可击的。只有当前提是错误的（错误地认为所有的羊都喜欢草），或者你的观察是错误的（正在观察的动物并不是羊），它才会出错。但如果这两件事都是正确的，而你的结论推理自你的前提，那么它在任何地方都是正确的，并且恒为真。

关于公理

演绎推理在数学中的重要性在古希腊时期就为人们所知，被誉为 “几何学之父” 的欧几里得提出了 5 个公理 (公设)，他认为这些陈述显然是正确的，不需要进一步的证明。

在欧几里得的数学世界中，他从这些选定的公理出发，严谨地推导证明出更多定理、不断拓展概念，将公元前七世纪以来希腊几何积累起来的丰富成果，整理在严密的逻辑系统运算之中，使几何学成为一门独立的、演绎的科学。

书中里面的一些定理，如勾股定理在任何地方都是正确的，这就是数学基于演绎推理的原因。证明是从你确信为真的命题中推导出要证明的命题的论据。

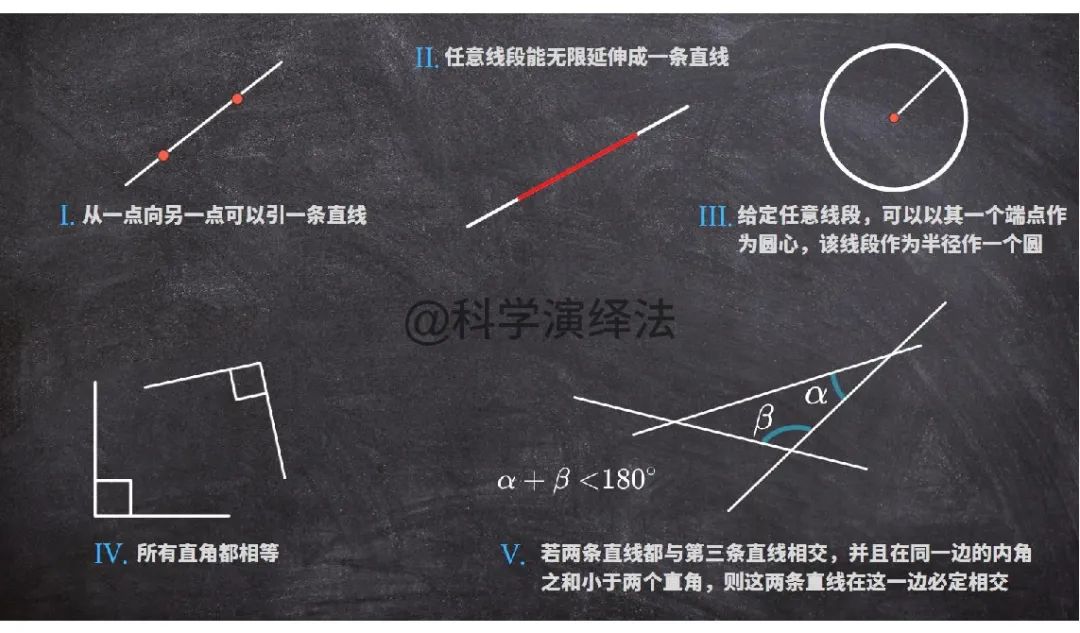
其中包括第 5 条公理又称为平行公设，它并不像前面四条公理那么简单明了，等价于这样的说法：三角形内角加起来等于 180°。这样的话，如果给你一个三角形中的两个角的大小，就可以利用一个平面中三角形内角和等于 180° 这一事实推断出第三个角的大小。

欧几里得认为任何其他关于几何的陈述，例如勾股定理，都应该通过演绎推理从 5 个公理中推导出来。他所作《几何原本》就是基于这种推理，也因如此，成为了有史以来最有影响力和最成功的书籍之一，在逻辑与现代科学发展进程中发挥了重要的作用。

但当然，你仍然需要非常小心地使用演绎推理，因为错误很容易溜进去。要确定结论是正确的，需要确保你的一般假设是正确的，并且您已经正确地使用了它们。

一个无效证明示例：

令 $a = b$ ，且

两边除以 $a$ 可得 $b = a$ ，Q.E.D.

例如，上面的那个无效证明只使用了关于如何处理方程的基本假设，但所得结论是错误的。你能找出其中的问题所在吗？

犯了除以零的错误。

我们需要证明吗？

为什么数学家坚持要证明一切呢？

比如，在法庭审判过程里，如果证据足够多，法官就很笃定给嫌疑人敲锤定罪，宣判其罪行已经被证明是 “无可辩驳的”。但冤案不是没有发生过，正义也迟来。

不过令人欣慰的是，数学也许是唯一可以绝对确定的领域，这就是为什么数学家如此重视证明的原因。此外，如果数学家不坚持证明的话，错误可能会悄悄出现，而问题很难被发现。

上面提到，欧几里得第 5 公理相当于说所有三角形的内角之和是 180°——他认为平行公理是如此明显，而无需证明，人们应该自然地接受它。

然而，在他之后的许多数学家们认为他们可以做得更好，试图从欧几里得前面 4 个公理中推导出平行公理，这样仅用 4 个公理就能建构出整个庞大的几何学体系。

数学家们为这一目标奋斗了几百年。在 19 世纪，它甚至成了一种给数学家下的魔咒，以至于匈牙利数学家鲍耶・法尔科斯 (Farkas Bolyai) 在挑战该问题失败后，觉得有必要严肃警告他的儿子鲍耶・亚诺什 (Bolyai János) 一定要远离它，别搭上自己大好的时光：

“看在上帝的份上，我恳求你放弃它。对它的恐惧丝毫不亚于感官上的激情，因为它也可能占用你所有的时间，剥夺你的健康、心灵的安宁和生活的幸福。”

▲ 椭圆几何、欧氏几何和双曲几何比较 (图自维基 @Cmglee 作品)

鲍耶・亚诺什还在坚持尝试，毫无疑问和其他人一样，也遭受到了失败的打击。但与他人不同，他由此怀疑平行公设并非总是正确的。只有当你在平面上画三角形时，它才能起作用。而如果把它画在一个球体上，比方说画在一个橙子上，内部角度加起来就超过 180°。在试图证明 180° 这一结果的过程中，数学家（包括亚诺什）偶然发现了另一个非常奇怪的曲面，称为双曲平面，在这个曲面上，三角形的角度加起来不到 180°。

双曲平面很抽象，但它类似于一片甘蓝叶，随着你向边缘移动，它会变得越来越皱。

虽然我们在日常生活中不会遇到这种奇怪的表面，但它是非常重要的。爱因斯坦的狭义相对论就是用双曲几何表述的。狭义相对论诞生了广义相对论，没有广义相对论，现代的卫星导航设备和具有 GPS 功能的手机都将无法工作。

数学证明还需要人类来做吗？

数学家常常引以为豪的事是，他们的研究只需要一支笔和一张纸就可以了。

但近几十年来，这种情况已经开始改变：计算机进入了数学领域，并引发了许多争论。这场争论与使用计算器或计算机进行奇怪的计算无关。数学家使用这些设备让他们的研究变得更容易，就像其他人一样。但这却让那些完全依赖于计算机的证明是否可信产生了新的争议。

有两种方式可以实现计算机证明：计算机辅助证明与自动化定理证明。

在计算机辅助证明 (computer assisted proofs) 里，计算机被用来执行大量的步骤，这些步骤是个人不可能在有限时间内完成的。1976 年，数学家凯尼斯・阿佩尔和沃夫冈・哈肯借助电子计算机首次完成四色定理的证明，这是计算机辅助证明的经典例子。证明的方法是将地图上的无限种可能情况减少为 1936 种状态，并由计算机对每个可能的情况进行验证。

当然，证明本身的逻辑仍然来自人类，但如果没人能够检查计算机处理过的所有计算，就不能百分之百确定证据中没有错误，所以有些数学家会认为这样的证明是无效的，仍努力寻找不借助计算机来完成证明。

近年来，计算机科学家还开发了自动化定理证明 (Automated theorem proving，ATP) 的计算机程序，它可以使用逻辑规则从一些基本前提推导出结果，从而证明它。到目前为止，ATP 仍然需要大量的人力投入才能正常工作，但可以想象，在未来，它们将变得更加强大。它们能否取代人类还有待观察，这是一个被激烈辩论的话题。

原文: https://plus.maths.org/content/brief-introduction-proof

数学中证明的魅力：建构逻辑体系的法宝

曹亮吉
遇见数学
2025 年 05 月 06 日 12:51 河南

作者 | 曹亮吉（当时任教于台大数学系）

转自 | episte.math.ntu.edu.tw/articles/sm/sm_16_02_1/index.html，原文标题《证明》，[遇见数学] 将术语调整至简体并补配图，转载请注明。

希腊的几何学一直到现在都还是正确的，我们都还在研读；现代人如果还有研读希腊物理学的，那也不过是基于历史的兴趣，因为它已经是不正确的。两者同样是希腊的产物，到头来为什么会有那么大的差别呢？

一套理论之所以能为人所接受是基于有说服人的能力。说服的方法可以是类比的、例举而加以归纳的、验证的，也可以是演绎的。中国古代的数学大都是例举的，而希腊在早期就奠定了演绎的方法。演绎分两部分，一部分是前题、假设或公理，是演绎的出发点，另一部分是证明，亦即从出发点推演到结论的过程。出发点真确，证明又严谨，结论才能正确。

▼ 古希腊数学家时间轴图 ([遇见数学] 制作)

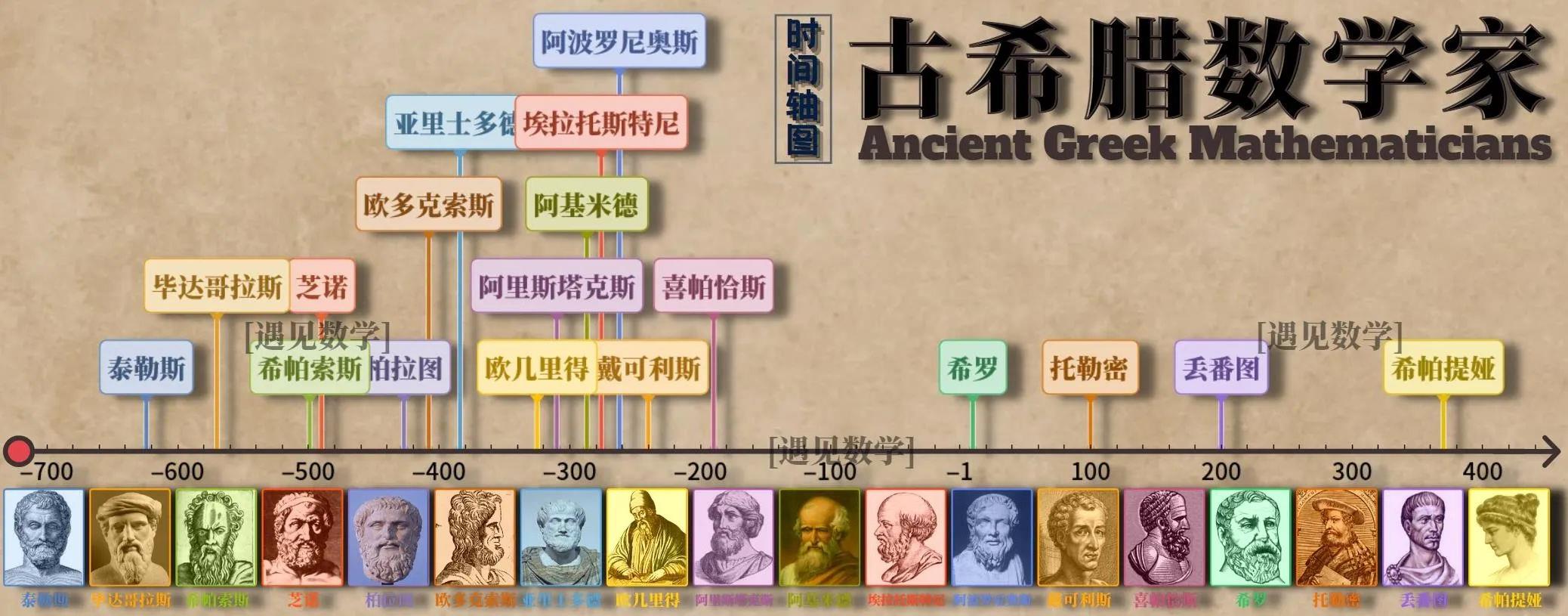
在这里插入图片描述

希腊从西元前六世纪的泰勒斯 (Thales) 开始注重推论的方法，到了亚里斯多德已经建立起严谨推论的逻辑方法。另一方面，希腊的数学家能够慎选几何学的出发点：点、线、圆及彼此之间的关系，而由欧几里得建立起正确严谨的几何学。欧几里得在其十三卷巨著《原本》中，由少数几个公理，用逻辑方法，证明了 465 个定理。反观希腊的物理学，因其基本假设的错误，再怎么严谨的逻辑也推演不出什么有意义的结论。由于几何学的成功，“证明” 成为数学的注册商标。于是数学离不了证明，更有甚者，“数学就是证明” 这种极端的想法也就相当流行。

数学中的证明，其最大的功用在于确立结论的百分之百正确性。根据百分之百正确的结论再证明而得的新结论也是百分之百正确。如此反复进行，所推得的各个结论，虽然离开最原始的假设甚远，也不用担心其正确性。

约翰・奥布里 (John Aubrey, 1626~1697) 在其《Brief Lives》中提到英国哲学家托马斯・霍布斯 (Thomas Hobbes, 1588~1679 年) 说：直到四十岁时，霍布斯才在一个偶然的机会中，接触到几何学。他在一个图书馆里无意中看到摊开的《原本》，摊开的地方正是原本第一卷第四十七个定理，那就是勾股定理。霍布斯的直觉反应是：怎么可能！于是他读了定理的注明，结果他发现这是根据前面的某个定理而推演出来的。于是他读了前面的那个定理，结果他又要读更前面的某个定理。如此继续倒着读，终于回到最原始也最直观的出发点。于是霍布斯相信了勾股定理，也爱上了几何学。这是说明演绎法之有说服力的一个最美丽的故事。

反观其他取得结论的方法，如类比、如例举，甚至臆测也可能得到正确度相当高的结论。但是如果这样的结论不是百分之百正确的，那么据之以再推得的新结论其正确性又要打折扣。如此，只要距离原始的假设稍远，结论的正确性，经过七折八扣，就几乎等于零了。

其次，证明的功用就像欧几里得的《原本》那样，在于把已知的许多数学知识做个有条有理的整理，使人理解整个体系的架构。当一个人熟知这些证得的数学知识后，他就可据之以证明新的结果，开拓新的领域。

由于证明有这么大的功用，于是 “证明了什么” 就成为衡量数学家的一种重要指标。譬如在 1984 年中，格尔德・法尔廷斯 (Gerd Faltings) 证明了莫德尔猜想，路易・德・布朗奇 (de Bourcia) 证明了比伯巴赫猜测，两人都因而声名大噪。

另一方面，为了表示功力，于是当你证明了什么就得赶紧发表，否则一旦别人的同样证明抢先发表，你就有抄袭之嫌。因此，为了 “谁先证明” 的问题，数学家可以打起官司来。再者，为了急于表示自己的成就，数学家也可能把证明出的一些不太有意义的结果赶紧送出去发表。

由于证明在数学上占有那么重要的地位，有关高等数学的许多课本往往也排满了定义、定理、证明、定义、定理、证明……，而数学的学习也往往循此方式进行。证明抽象程度有层次之分，学习者层次较低或书本的层次较高，都造成学习的障碍。有些书上常用 “这是显而易见的 (it is trivial 或 it is clear)” 这样的字眼，但可能读者再怎么看都不觉得其明显。

辅助线不知怎么来是另一类使人困扰的问题。在证明的过程中，我们往往遇到 “越轨” 的方法，几何证明辅助线是令人难忘的例子。要证明 $x^2+y^2=z^2$ 除 $(0, 0, 0)$ 外无整数解，你就得超出整数范围，到高斯整域求援；要证明 $x^3+y^3=z^3$ 无非零整数解，你就得求诸于代数数论的方法。实函数积分往往要看成复数积分的一部分才能求出，等等。例子多得不胜枚举。等你习惯了之后，或许你会体会到数学是一体的，“越轨” 似乎是常态，正也是数学吸引人的地方。

再者，面对这一类型的课本，读者纵使把书上每个定理的证明弄懂，对整本书的重点是否把握得住也不无问题。

其实数学并不就是证明。我们只知道牛顿创造了微积分，未曾听说过微积分中那个定理是牛顿证明的。微积分基本定理吗？牛顿是第一个了解到这个定理的重要性的人，但以现代的标准而言，直到十九世纪把实数、函数、极限、微分、积分的概念弄清楚之前，微积分基本定理的证明是无从进行的。我们说牛顿创造了微积分，因为他承继了前人零碎的知识，有系统地发展了微分的技巧，将微分与积分经由微积分基本定理联在一起而合流成微积分，又将微积分成功地应用到物理上。在这种创造的过程中，当然免不了要有些证明，但证明可能不严格，也不是最重要的。到了现代，数学的证明愈来愈讲求严格，但和从前的一样，寻找有意义的定理才是数学创造的泉源，而证明有意义的定理才会带给数学有意义的发展。

创造理论固然比证明定理重要，但如果能证明出一连串相关定理也许也就创造了某种理论。另外，证明定理可以说是数学家磨练能力的最好办法。在磨练的过程中，若能一方面增强实力，一方面扩展视野，有朝一日也许也会走上创造理论的道路。

每一种理论总有一些核心的定理，能够证出这些定理当然是功德圆满，功成名就。有些问题，因为长久不得解决，招来许多数学名家想要把它证明而后快，因此变得非常有名。譬如质数分布定理花了一百年才得证，四色定理一百多年；费马大定理历三百年不得解决，黎曼猜想也有一百多年的历史。

黎曼猜想关系到数论的许多问题，是解析数论中的核心问题。许多数学家没耐心等待该猜测之得证，早已把它当做是对的，而以它为基础，讨论其他的数论问题。质数分布定理固然也很重要，但与黎曼猜想相比就小号多了，因为较弱形的黎曼猜想就可以导出质数分布定理。费马大定理本身得证，也不会使数论有所改观；倒是因为长久以来，数学家为了证明它而发展了代数数论，因此这个问题就变得很有名，而能否将它证明也变成大家关切的焦点。四色定理之有名也和费马大定理类似：本身不重要，但长久不得解决，且为了解决它而图形理论有长足进步。

另外还有一类问题，长久以来都无法证明，最后数学家才恍然大悟，原来它们是无法证明的。平行公理是最有名的例子。经过二千二百年之久，数学家才领悟到平行公理是无法由其他的欧氏平面几何公理推演出来的，因而创造了非欧几何；非欧几何的存在正证明了平行公理是不可能证明的。三大几何作图题，五次以上方程式的根式解等都是属于这一类 “非不为也，是不能也” 的问题。一旦数学家领悟到某个问题的证明是 “非不为也，是不能也” 的，那么我们就可以期待数学发展会有新的气象。

有些定理会经数学家一再用不同的方法证明。勾股定理起码有 370 种证法，好奇、好玩的成分居多。对证明严谨的要求逐渐提高，也使许多定理的证明一再回炉重炼，狄利克雷原理就是个例子。高斯对代数学基本定理先后提出三种证法，对二次互逆律先后提出七种证法，其目的则是想从不同的角度来看这些定理，希望能证得更简单些或希望其中有些证法可以推广到更复杂的情形。

一个定理的证明经人提出来了，怎样判定它是对的还是错的？一年出产的定理有几十万个，一个人不可能一一再确定，我们只能信任内行人的判断。通常把证明写成初稿送请同行批评指教，然后再写成定稿送到期刊去。期刊编辑会请行家判断其正确性（当然更要判断论文的价值）；刊出后，数学评论会请人为文作评论，如果经过这些手续后，没有人说它有问题，其他的数学家也就相信它的正确性，也会开始加以引用。其中较重要的定理日后就成为一般的数学知识，甚至一般的数学家也能重复它的证明。

有时候因为证明过于复杂，这种征信手续也不免引人忧虑。1976 年阿凯尼斯・阿佩尔 (Appel) 及沃夫冈・哈肯 (Haken) 用电脑帮助证明了四色定理后，马上引起许多人的谈论。“谁有耐心、能仔细检查那些又长又枯燥的电脑程式及其计算结果？” 就是谈论的重点之一。前几年，有限单纯群的分类宣告完成时又引起了一阵骚动，因为整个分类工作并不是在一篇论文中完成的，而是行家根据十几年来的进展，从散在各个期刊中有关这方面的论文，归纳出分类确实已经完工。根据有限单纯群的行家丹尼尔・葛仑斯 (Gorenstein) 的估计，要了解整个分类，有关的文献就有五千页之多。大家担心的是：万一其中一篇论文有些许错误，那么大局是否受到影响？

由于证明在数学中的重要性，因此与证明有关的话题非常多。下一次，我们将就存在型及建构型两类证明方式，做较详细的讨论。