高速系统设计理论基础

如前一章所述，在进行高速系统设计时，最重要的是要从基本理论出发，只有掌握了基本理论，然后才能谈到其他的设计技术和技巧。本章主要介绍微波电磁理论基础，及其在高速系统设计中的工程化分析方法和应用。通过对微波信号在高速系统中的现象分析，使我们更清楚地理解高速系统不同于传统系统的一些特殊现象，从而为更好地理解信号完整性打下良好的基础。

2.1 微波电磁波简介

微波是频率非常高的电磁波，国际上，它的频率范围目前尚无统一的明确规定。

通常，我们将频率为300MHz至300GHz的电磁波称做微波，将30GHz至300GHz的电磁波称做毫米波，相应的电磁波频段称做微波、毫米波频段。将频率在300GHz至3000GHz的电磁波称为亚毫米波。亚毫米波和微波具有类似的特征和相近的分析方法。一般地说，微波在电磁波频谱中所处的位置在特高频（UHF）和光波之间。

根据电磁波频率、波长与速度的关系f×λ=3×10^8 m/s可知，微波的波长范围在1m至0.1mm之间。整个微波频段又按照波长划分为几段，它们如表2-1所示。

对于微波频段的划分和命名，国内外有多种方法，表2-2给出了在雷达和制导技术领域划分微波频段的方法及其频段代号。

微波在电磁波频谱中所处的位置决定了它的许多特点，并使得微波技术具有许多不同于低频电路理论和光学理论的概念及独特的分析方法。不同工作频率的微波系统具有不同的技术特性、生产成本和用途。一般来说，对于微波通信系统而言，工作频率越高，其结构尺寸越小，生产成本越高，信息容量越大，但同时，其大气传输和传输线传输的损耗就越大。

这里我们介绍了一些微波的基本概念。那么微波传输理论和本书要介绍的高速系统设计有什么关系呢？我们知道，按照信号理论，一个理想的周期方波信号从频域上看，是由无穷多个倍频信号组成的。各倍频信号的能量也不尽相同，倍频信号的频率越高，其能量越小。如图2-1所示，左图是一个理想周期方波信号，右图是该信号的频谱分布。

 按照一般的设计分析需求，截取到5倍频信号能量就可以了（包含了原信号中大约90%的能量）。所以，当信号的上升（下降）沿的时间越短，越接近理想的方波信号，其含有的频谱分量就越丰富。举例来说，125MHz的时钟信号，其5倍频信号频率为625MHz；而对于DDR的200MHz时钟信号，其5倍频信号频率为1GHz。这些信号的5倍频信号都已经进入到了微波频段，更不用说2.5Gbps，甚至3.125Gbps，6.25Gbps的高速串行信号了。对这些信号特征的分析，必须使用微波理论分析技术，才能够比较精确地预测信号行为，指导高速系统设计。

2.2 微波传输线

微波能量的传输系统与低频电磁能量的传输系统不同。例如，微波对天线与真空、大气可以构成微波传输系统，微波传输线也是微波传输系统。微波传输线主要包括同轴线、金属波导、介质波导和微带线等。微波传输线的损耗一般都比较大，不适于长距离传输微波能量。

对于工作波长为3cm（工作频率约为10GHz）的矩形金属波导，微波能量沿该波导传输1m距离，将衰减0.3～0.44 dB。也就是说，微波能量沿该波导每传输1m距离，微波能量就要损失约10%；对于工作波长为3mm（工作频率约为100GHz）的矩形金属波导，微波沿该波导传输1m距离，将衰减2.35～3.34 dB。也就是说，微波能量沿该波导每传输1m距离，就要损失约50%的能量。因此，波导传输系统不适于长距离传输微波信号和微波能量。微波在大气中的传输损耗远远大于其在传输线中的传输损耗。由于微波大气传输损耗的衰减机理主要是水分子和氧分子对微波能量的共振吸收，因此，微波工作频率或海拔高度不同，微波传输损耗也不同。在电磁波频谱中，微波的位置处于特高频和光波之间。

研究低频电磁波系统的理论有：电磁学和电子线路等，研究光波的理论和几何光学和波动光学等，研究微波的理论是微波技术。概括地讲，微波技术包含两种基本分析方法，分别介绍如下。

1. 经典电磁理论

微波技术的基本研究方法是“场解法”。场解法就是在一定的边界条件下，求解麦克斯韦方程组。从理论上讲，所有微波技术中的问题都可以用“场解法”求解。遗憾的是，除了在非常简单的边界条件下，我们可以得到封闭的场解，在某些边界条件下，可以借助电子计算机得到数值解外（计算电磁学），在大多数的边界条件下，我们不可能得到封闭的场解。同时，由于麦克斯韦方程所需要的数学复杂性（场解给出的是空间中任何一点的电磁场的完整描述，它提供的信息比大多数实际工程中需要的要多），使得在工程应用中，我们不可能，也没有必要对每个微波相关问题都列出麦克斯韦方程并去求解这个方程。

2. 微波等效电路理论

在微波工程应用领域中，需要有简便的工程计算方法。在一定的条件下，类比于低频电路的概念，因此可以将本质上属于场的微波电路转化为微波等效电路，从而使微波工程的计算和分析得到简化。

对于大多数微波工程问题，我们不可能得到封闭的场解。所以，在解决微波工程问题时，需要在基本理论、基本概念和近似计算的指导下，进行大量的实验和调试。

因此可以说，基本概念和实验技能是微波技术的基本内核，清晰的基本概念和熟练的实验技能是微波工程技术人员应该具备的基本素质。

2.2.1 微波等效电路物理量

由于微波波长较短，微波的传输系统、微波元器件及它们的工作原理和分析方法都与直流、低频电路系统、低频元器件及它们的工作原理和分析方法截然不同。

首先，我们在分析低频电路时，可以认为有关物理量在传输系统中是均匀分布的。因此，我们只需考虑各物理量随时间的变化，而不考虑其空间分布。

对于微波系统，我们必须同时考虑各物理量随时间的变化及其空间分布。在确定的空间内，对于低频信号我们观察到的是物理量的振荡，对于高频信号我们观察到的是物理量的波动。例如，电磁波的频率为50Hz，其波长即为6000km；电磁波的频率为100GHz，其波长就只有3mm。

一般来讲电路的尺度为几十mm，分立元件的尺寸为几个mm，当频率较高的电磁波通过时，在分立元件的两端，该信号的一些物理量就会发生变化。因此，对高频信号的分析，就必须考虑电磁场的空间分布。由于微波的特点，微波电路不但采用了与低频电路不同的传输系统，而且在分析微波电路时也必须引入与低频电路不同的物理量，低频电路系统与微波电路系统的比较如表2-3所示。

 2.2.2 微波传输线等效电路

长线理论是微波等效电路理论中涉及单模均匀传输线传输特性的理论。在这里必须注意，我们的研究对象是微波，由于微波的波长很短，因此在很短的一段传输线上，微波的相位就会有明显的差异。频率为50Hz的低频交流电，在传输线上的相位变化是6×10^-5度/米（波长6000km）；而频率为10GHz的微波，在传输线上的相位变化是1.2×10^6度/米（波长3cm）。

因此，在研究低频电路时，一般不考虑相位问题，在讨论微波电路时就必须加以考虑。如图2-2是我们用电路方法分析微波传输线的等效电路及参考方向的过程。

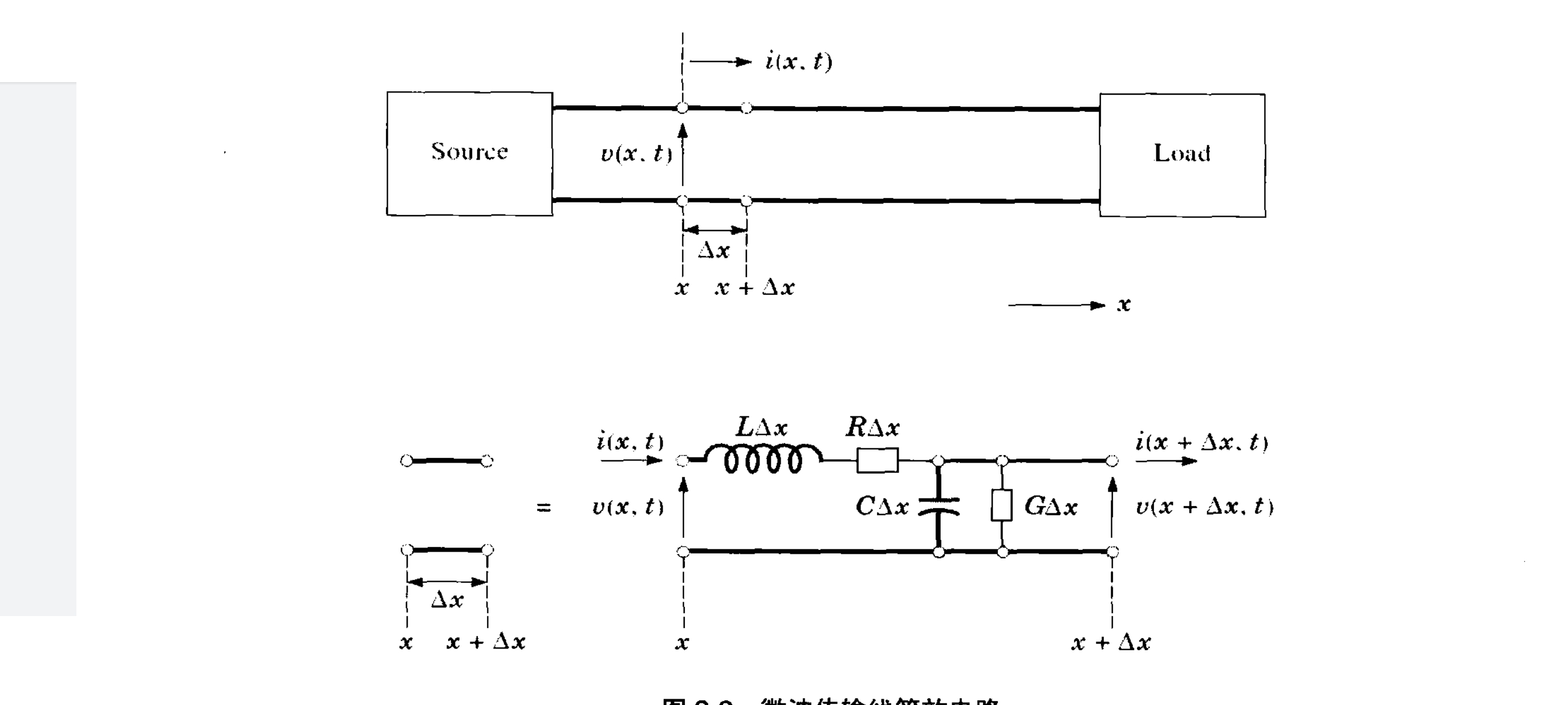
传输线方程（电报方程）及其解

根据图2-2的等效电路，在长度为dx的一段均匀传输线上的串联阻抗和并联导纳可以表示为：

Z=R+jωL(2.1)

Y=G+jωC(2.2)

R 为单位长度导体的串联电阻，Ω/m；L 为单位长度导体的串联电感，H/m；G 为单位长度导体的并联电导，S/m；C 为单位长度导体的并联电容，F/m。

根据电路分析理论中的基尔霍夫定律（分流、分压关系），可以得到电压波和电流波的微分方程组：

Δv(x,t)=v(x+Δx,t)-v(x,t)=(-R*Δx)Δi(x,t)+(-L*Δx)*{di(x,t)/dt(2.3)

Δi(x,t)=i(x+Δx,t)-i(x,t)=(-G*Δx)*v(x+Δx,t)+(-C*Δx)*dv(x+Δx,t)/dt(2.4)

式(2.3)、(2.4)就是长线理论的基本方程——电报方程。

整理上述两式，除以Δx，并利用Δx->0，得到如下两个方程：

dv(x,t)/dt=-R*i(x,t)-L*di(x,t)/dt(2.5)

di(x,t)/dx=-G*v(x,t)-C*dv(x,t)/dt(2.6)

对式(2.5)进行dx求导，对式(2.6)进行dt求导，得到如下两式。

d^2v(x,t)/dx^2=-R*di(x,t)/dx-L*d^2i(x,t)/dx^2(2.7)

d^2i(x,t)/dt^2=-G*dv(x,t)/dt-C*d^2v(x,t)/dt^2(2.8)

将式(2.6)和(2.8)代入到式(2.7)中，消除di(x,t)/dx和d^2i(x,t)/dt^2，得到如下波动方程式：

d^2v(x,t)/dx^2-γ^2*v(x,t)=0(2.9)

这里γ=√(R+jωL)(G+jωC)}=α+jβ

其中，α是单位长度上的衰减常数（奈培）；β是单位长度上的相位常数（弧度）。

在不考虑时间量的情况下，式(2.9)的通解为：

v(x)=V+*e^-γx+V-*e^xγ(2.11)

式(2.11)也给出了在传输线上传输的一般表达式。前向传输的电压表示为V+*e^-γx，反射（后向）传输电压为V-*e^γx。V(x)是x点处，前向传输电压和反射电压之叠加。

按照同样的求解过程，我们可以得到关于电路的方程式：

i(x)=I+*e^-γx-I_*e^γx(2.12)

从而得到：

I+=V+*γ/(R+jωL),I-=V_*γ/(R+jωL)  (2.13)

在取得传输线上的电压和电流表达式后，很容易就得到了传输阻抗的表达式：

Z0=V+/I+=V_/I_=(R+jωL)/γ=√[(R+jωL)/(G+jωC)^](2.14)

对于无损传输线，即R=G=0，则阻抗和传播系数的表达式为：

Z0=√(L/C)，γ=jβ=jω√(LC)(2.15)

由阻抗表达式(2.14)和(2.15)可以看出，对于理想传输线，其阻抗和信号频率无关，而对于有损传输线，阻抗和频率相关。但是由于我们所研究的信号频率比较高，并且传输线上的电阻和电导效应比较微弱，一般情况下：

R≤jωL,G≤jωC

在这种情况下，表达式(2.14)可以近似等于(2.15)，因此对于损耗不大的有损传输线也近似等效成无损传输线。

通过以上的分析，我们得到了有损（无损）传输线的阻抗表达式(2.14)，该表达式是我们分析高频电路的最基本出发点，在接下来的高速电路分析和设计中，很多物理现象的分析及问题的解决都和传输线的阻抗表达式密切相关，希望读者能够理解并且牢记该表达式，以及表达式中各个参数所代表的含义。

2.3 电磁波反射

如图2-3所示，我们知道，电磁波是通过电磁场在传输介质中交替建立电场和磁场进行传播的。在均匀介质中，这样的电磁场交替建立会一直沿着传输方向持续下去，虽然电磁场的强度会按照一定的衰减系数衰减，但是不会改变电磁场的交替建立方式及传播方向。但是如果电磁波遇到障碍物（所谓障碍，是指传输介质的传输特性发生变化），电磁场的交替建立过程不能顺利延续下去，那么电磁波就会改变其传输方式。对于图2-3中示例的TEM波而言，由于电磁波的传输方向已经被限制在Z轴方向，那么一部分电磁波会按照原来的方向继续传播，而另外一部分电磁波就会沿着Z轴向回传播，这一部分电磁波就是反射。

c=f*λ=3*10^8m/s

因此，简单的理解就是，当微波在介质上进行传输时，如果遇到障碍，即阻抗不连续的非均匀传输介质，将会产生很强的反射。电磁波的传输和反射现象是高速电路的最基本现象，研究和理解微波在其特定传输介质上的反射现象，对于我们理解高速信号在系统中的传输特性，设计出稳定可靠的高速系统非常有帮助，这也是研究其他高速设计问题的基础和出发点。

在如图2-4所示的电路结构中，X=0处是均匀传输线和负载Z的边界。从上一节的定量分析结果，我们可以得到，此处的电压和电流表达式为：

V0=V0++V0-(2.16)

I0=I0+-I0-(2.17)

由于该均匀传输线的特征阻抗为Z0，有如下等式：

I0=I0+-I0-=V0+/Z0-V0-/Z0(2.18)

同时，在该点处，从负载的角度看，总电压和电流必须满足：

ZL=V0/I0=(V0++V0-)/I0(2.19)

将式(2.18)代入到(2.19)式中，得到：

ZL=(V0++V0-)/I0=[(V0++V0-)/(V0+-V0-)]*Z0(2.20)

进一步得到如下关系：

V0-/V0+=(ZL-Z0)/(ZL+Z0)=ρ1(2.21)

从式(2.21)出发，我们定义反射电压和前向传输（入射）电压之比为反射系数，即当在微波的传输路径上发生阻抗不匹配时，由此产生的反射电压和前向传输（入射）电压之比。由此可知，在微波传输路径上发生的反射强度是由传输线和负载的匹配程度决定的。

同理可以导出，当信号源内阻和传输阻抗不匹配时，同样也会发生反射，其反射系数为：

ρ1=(ZS-Z0)/(ZS+ZL)(2.22)

有很多工程师在谈到匹配的时候，通常会默认为终端匹配。事实上正如上式中所证明的那样，源端也同样存在匹配问题。一般来讲，终端匹配更加重要，因为这是消除反射的最佳位置。但是在很多情况下，终端不允许做匹配或者终端匹配机制做得不好，那就要在源端进行匹配，来消除反射。这一点读者一定要理解清楚，终端匹配和源端匹配并不矛盾，只是匹配的位置和消除反射的对象有所不同。

在实际工作中，读者可能经常看到时钟芯片的输出管脚，一定要加一个22Ω或者33Ω的串联电阻，这就是非常典型的源端匹配。

2.4 微波传输介质

正如上一节中所讲的，微波信号的反射是由于传输介质的阻抗不连续所引起的。因此，为了研究工程中信号的传输质量，我们就不能不研究微波传输介质。

微波传输系统有很多，不同的传输系统具有不同的电气特征，适合不同模式的电磁波传输。表2-4中是几种典型的微波传输系统的比较。

 在本书中，由于我们只着重于PCB电路系统的设计技术，因此这里我们讨论和PCB密切相关的两种微波传输系统：微带线和带状线。而最适合在微带线和带状线上传输的电磁波是TEM波，其电磁场结构如图2-4所示，电场和磁场相互垂直，并都垂直于传输方向Z轴。

微带线也是一种双线传输系统，它的基本结构及TEM电磁波在微带线上的电磁场分布情况，如图2-5所示。它与常规双线传输系统的区别在于：两导体之间的距离非常近（相对于工作波长），同时，由于在PCB系统中，微带线的其中一个导体，也就是参考地平面，通常以一个公共导电层的形式出现，使得很多设计者反而忽略了这个导体的存在。久而久之，就形成了一个错误观念，认为微带线就是单导体传输系统。微带线具有工作频带宽、体积小、重量轻，可以构成微波集成电路等优点，但和其他微波传输系统相比缺点是损耗较大、功率容量较小。

2.4.1 微带线 Microstrip Line

在PCB中，微带线是一种用电介质将导线与接地面隔开的传输线。印制迹线的厚度、宽度和迹线与接地面间介质的厚度，以及电介质的介电常数，决定微带线特性阻抗的大小。

微带线的几何结构如图2-6所示，导带的宽度W印在薄的、接地的介质基片上。

实际上，微带线的准确场是一个混合TE-TM波，需要更加先进的分析技术。但在大部分的实际应用中，介质基片电气上很薄，Ez和Hz在其波的传输方向上的分量非常小，可以忽略，所以微带线电磁场是准TEM波。换句话说，电场本质上与静电场是相同的，因此，通过静态或准静态解，可得到相近的相速、传播速度和特性阻抗。

根据《IPC-2141 Controlled Impedance Circuit Board and High Speed Logic Design》规范，推荐工程使用的微带线参数计算公式如下。

特征阻抗：

Z0=87/√(ε+1.41)*ln5.98h(0.8W+t)(Ω)(2.23)

传播延迟：tpd=85√(0.457ε+0.67)(ps/inch)(2.24)

等效电容：C0=1000*tox/Z0(pF/ft)(2.25)

等效电感：L0=Z0^2*C0(pH/ft)(2.26)

对普通FR-4材料（介电常数ε在4.5～5之间）：750微带线结构中，W≈h；50Ω微带线中，W≈2h。

微带线的宽度W越大，微带线的特性阻抗Z0越低。近似公式在微带线宽度W远大于介质厚度t时精度较高，否则，就需要加以修正。当W与t相当时，误差约为百分之几到百分之十几。其中微带线宽度W远大于介质厚度t也正是目前PCB工艺所能实现的。

需要说明的是，实际上微带线的特性阻抗Z0、传播延迟tpd，都是工作频率的函数。因此，需要注意的是，当工作频率升高时，微带线的色散将增大，基于准静态分析法的近似公式的精度将变差。因此，在毫米波频段，微带线电路的理论计算比较困难，一般认为频率f<4GHz时，可以忽略色散效应，同时，实验表明，工作频率f升高，等效介电常数ε将增大，所以当微带线的工作频率较高时，特征阻抗Z0、传播延迟tpd的频率响应将不可忽略。

2.4.2 微带线的损耗

对于微带线损耗的精确计算只能采用数值解，计算过程相当复杂，微波工程中通常采用近似公式和经验公式来估计微带线的损耗。以下对微带线的损耗做定性的讨论，以得到概念性的了解。

微带线的损耗可以分为三类，导体欧姆损耗、介质损耗和辐射损耗。

1. 微带线导体表面的欧姆损耗

在传输功率一定的条件下，微带线导体表面欧姆损耗的一些基本特点如下。

• 如果介质基片的厚度h减小，则两导体之间的磁力线密度增大，损耗将增加；

• 如果导体表面的光洁度下降，或导体的电导率σ减小，损耗将增加；

• 在微带线导体表面光洁度和工作模式一定的前提下，由于趋肤效应的存在，随着工作频率升高，微带线的损耗将增加。

2. 微带线的介质损耗

微带线的介质损耗来源于复介电系数的虚部，其物理机制是介质中的漏电导离子、电子在微波激励下的热振动等。在微波工程中实用的电介质材料的介质损耗都相当小，以最普通的微波介质材料氧化铝（Al2O3）为例，当其纯度为96%时，其介质损耗仅为欧姆损耗的1/6；当其纯度为99.5%时，其介质损耗仅为欧姆损耗的1/36。

因此，在估计微带线的损耗时，一般情况下可以不考虑微带线的介质损耗。

3. 微带线的辐射损耗

若微带线导体带的宽度W→∞，则电磁波成为两个无限大导体平板间的导行电磁波，这时就没有辐射损耗。所以，导体带的宽度W越小，则微带线的辐射损耗越大。

辐射不但会形成损耗，还会对周围系统带来干扰。

微带线的设计和应用主要应当从以下几个方面考虑。

1. 加大介质厚度h、减小导带宽度W，提高导体和介质基片的表面光洁度，可以减小微带线的欧姆损耗。但是，加大介质厚度h、减小导带宽度W，将增加微带线的辐射损耗。因此，应当综合考虑欧姆损耗和辐射损耗，以便选择介质厚度h和导带宽度W的最佳值。

2. 微带线几何参数介质厚度h、导带宽度W的确定，不但要考虑损耗的因素，还要考虑到单模传输条件、微波与表面波的耦合频率、特征阻抗、传播常数等因素。

3. 由于微带线的损耗较大、功率容量较小，因此它通常是用于微波电路内部的传输线，不宜作为微波系统之间的传输线。也可以用在芯片内部、板上芯片间的互连。

2.4.3 带状线 Strip Line

带状线是一条置于两层导电平面之间的电介质中间的铜带线。如果线的厚度和宽度、介质的介电常数及两层导电平面间的距离是可控的，那么线的特征阻抗也是可控的。带状线的几何结构如图2-7所示。

根据《IPC-2141 Controlled Impedance Circuit Board and High Speed Logic Design》规范，推荐工程使用的微带线参数计算公式如下。

特征阻抗：

Z0=(60/√ε)*ln[(4h/0.67πW(0.8+t/W)](Ω)(2.27)

传播延迟：tpd=85√ε,(ps/inch)(2.28)

等效电容：C0=1000*tox/Z0(pF/ft)(2.29)

等效电感：L0=Z0^2*C0(pH/ft)(2.30)

对FR-4材料（ε在4.5～5之间）；75Ω带状线，W=h/8；50Ω带状线，W=h/3。

对于带状线参数特性分析，包括基本损耗特性等，基本和微带线相同，可以直接使用微带线的分析结论和结果。在此，不再重复。

2.4.4 同轴线 Coaxial Line

为了避免微波能量的辐射损耗，人们首先想到的是，采用具有封闭形式的双导线传输系统——同轴线。同轴线将电磁场完全限制在内、外导体之间，因而消除了辐射损耗。同轴线是由传输线内芯及包裹在外部的电磁屏蔽层构成，在内芯和屏蔽层之间填充一定材料的绝缘介质，其几何结构如图2-8所示。

 

了解了同轴传输线的物理结构，也就不难理解它的等效电路模型，如图2-9所示。

同轴线可以说是由双导线传输系统演变来的。随着微波系统工作频率的提高，为了保证单模传输，同轴线的横截面尺寸必须大大减小，这就产生了新的问题，

• 同轴线横截面尺寸的减小，使得同轴线的欧姆损耗增大，这种损耗主要来自内导体表面。

• 同轴线横截面尺寸的减小，使得在相同电压条件下，同轴线内电场强度增大，因而容易产生击穿现象，而且击穿将首先发生在内导体表面。

• 由于这两个条件的限制，同轴线不能工作在高频和大功率条件下。

对于同轴线的特征阻抗和传播延迟不再推导，直接给出公式如下。

特征阻抗：Z0=(60/√ε)lnD2/D1(Ω)(2.31)

传播延迟：tpd=85√ε,(ps/inch)(2.32)

2.4.5 双绞线 Twist Line

双绞线是我们熟知的一种传输线结构，也正是由于在日常生活中普遍存在，因此我们不怎么关注，事实上它也是一种微波传输线，它的几何结构如图2-10所示。

双绞线的特征阻抗和传播延迟公式如下。

特征阻抗：Z0=(120/√ε)ln(2S/D)(Ω)(2.33)

传播延迟：tpd=85√ε(ps/inch)(2.34)

读者应该会注意到，由于双绞线的制作规格比较松散和实际滥用的情况，使得双绞线的介电常数ε和线间距S得不到严格保证，这也影响了它在微波领域的应用。事实上，如果能够在生产加工的过程中严格控制双绞线的参数，还是能够使它在一定的条件下用于微波信号的传输的，例如，用于千兆位以太网的CAT5双绞线和万兆位以太网的CAT6双绞线就是一种典型用例。

2.4.6 差分传输线

近年来，随着高速信号技术的发展，对高速信号的传输提出了更多的要求，比如低损耗、低功耗及抗干扰等。差分传输线独特的传输特性使它在高速串行信号传输领域得到了广泛的应用，差分传输线的几何结构如图2-11所示。

和单端传输线一样，差分传输线也有微带线和带状线两种形式。其等效电路模型和分析方法和单端传输线基本一致。

当在这样相邻的两条传输线上进行高速差分信号传输时，会有两种情况。

1. 差模信号方式

如图2-12的上图所示，信号驱动端发出的是极性相反的信号：Vp和Vn。

此时在这两条传输线上的传输电流为：

i1+k·i2和i2+k·i1，其中k为两条差分传输线的互耦合系数。

因此，这两条传输线中的任意一点的电压为：

V1=Z11·(i1+k\·i2)=Z11·i_1+Z11·k·i2(2.35)

V2=Z22·(i2+k·i1)=Z22·i2+Z22·k·i1(2.36)

Z11和Z22为两条传输线的特征阻抗。经过仔细的设计，使两条传输线的各参数平衡的情况下，我们有：

• i1和i2，大小相等，方向相反，i1=-i2；

• 单线阻抗Z11=Z22=Z0，Z0即上几节中提到的单端传输线特征阻抗。

此时，式(2.35)和(2.36)变为：

V1=Z0·i1(1-k)=Z0·i1(1-k)(2.37)

V2=Z0·i_2(1-k)=Z0·i2(1-k)(2.38)

因此，在这种传输模式下，从单个传输线的角度来看，差分模式下的传输线的特征阻抗如下式表示：

Zodd=V1/i1=V2/i2=Z0·(1-k)(2.39)

2. 共模信号方式

如图2-13上图所示，与差模传输方式不同的是，信号驱动端发出的是极性相同的信号：Vp。

此时这两条传输线上传输的电流为：

i1+k·i2和i2+k·i1，其中k为两条传输线的互耦合系数。

此时，这两条传输线中的任意一点的电压为式(2.35)和(2.36)所表示的关系。

同样经过仔细的设计，使两条传输线的各参数平衡的情况下，我们有：i1和i2，大小相等，方向相同，i1=i2，这是和差模信号方式不同之处；单线阻抗Z11=Z22=Z0，Z0即上几节中提到的单端传输线特征阻抗。

此时，式(2.35)和(2.36)变为：

V1=Z11·i1(1+k)=Z0·i1(1+k)(2.40)

V2=Z22·i2(1+k)=Z0·i2(1+k)(2.41)

然而，需要读者特别注意的是，此时，由于共模信号方式在两条传输线上各点分布的是同极性电压，而且是同向电流，因此，共模信号方式下，每条传输线的回路是真正的地平面。两条传输线之间，除了耦合之外，是相对开路，即独立状态。而在差模信号方式下，两条传输线之间建立紧密合地场模式，相互作为回路参考平面，从而使得其中一条单线上的电流会沿着另外一条传输线反向流回，在电气回路上不需要参考地平面参与，造成参考地平面成为虚设，也就是人们常说的虚地状态。

这样，按照以上的分析，共模信号方式下，流入地端的电流是两条传输线上的电流总和。因此共模信号的传输阻抗为：

Zeven=V1/i1+i2}=V1/(2i1)=1/2·Z0·(1+k)(2.42)

2.4.7 差分阻抗

通过以上的分析，我们了解了在差分传输线中信号的传输特征，以及信号方式的不同会使得差分传输线的阻抗也不同。但是读者需要注意的是，以上的分析是分别建立在差模信号和共模信号相互独立的基础上的。而在实际应用中，差分信号以如下的方式进行传输。

差分信号驱动端发出的信号是：

Vp=Veven+1/2·Vdiff(2.43)

Vn=Veven-1/2·Vdiff(2.44)

驱动端输出的信号同时具有共模和差模信号分量，是差模信号和共模信号的混合模式。而在接收端输入的有效信号则是：

Vout=Vp-Vn(2.45)

这样，我们可以看出，每根个传输线上只具有一半的差分信号能量，其差模传输阻抗为Zodd=Z0·(1-k)。所以从整个要传输的差分信号Vdiff的角度来看，其传输阻抗就应该为单线差模阻抗的两倍（因为实际的单根传输线上的传输电流没有改变，而最终接收端收到的差分信号逻辑为的Vdiff，即：

Zdiff=2·Zodd=2·Z0·(1-k)(2.46)

这也就是人们常说的以“50 Ω 单线传输阻抗设计出 100 Ω 的差分阻抗”。

工程上，人们普遍使用的差分阻抗计算公式为：

微带线差分阻抗，Zdiff=2·Z0[1-0.48·e^(-0.96·s/h)](2.47)

带状线差分阻抗，Zdiff=2·Z0[1-0.347e^(-2.9·s/h)](2.48)

2.5“阻抗”的困惑

这是一个耐人寻味的话题。

虽然在前面几节中，我们已经开始大量使用了“阻抗”这个词，但是未必所有的读者都能够理解它的含义。实际工作中，经常可以听到一些有关传输线“阻抗”的似是而非的说法。

例如，对于如图2-14中所示的一段微带线来说，关于微带线A的“阻抗”，不同的人会给出不同的解释，根据作者多年的教学经验，这些解释基本上可以分成三类。

1. 微带线A的“阻抗”为零，因为它是一段铜线，可以认为为零；

2. 微带线A的“阻抗”为无穷大，因为它的末端开路；

3. 微带线A的“阻抗”应该为Z0，正如公式(2.23)所表示的那样。

那么，读者们该怎么认为呢？

这是个很普遍的问题，它不仅困扰一般的从事电子工程工作的技术人员，即使对于从事高速系统设计的电子工程师，也经常会为这个问题所“迷惑”。在给出进一步的说明之前，我们先来回顾一下几个基本概念的定义。

2.5.1 阻抗的定义

对于所有的理想元件，其阻抗定义为该导体两端的电压和流经该导体的电流的比值，如图2-15所示。这个定义不论在时域还是频域，在任何情况下都是有效的。

从这个定义出发，对于理想电阻，其电压和电流总是同频矢量，因此，理想电阻的阻抗和频率无关，也就是电阻本身的阻值。对于这一点，应该是所有电子工程师的共识。而对于电感感抗和电容容抗，则分别有：

ZL=VL/IL=L·(dIL/dt)/IL=L·[(d(I0·e^jω)/dt)/(I0·e^jω)= jωL(2.49)

ZC=VC/IC=C·[VC/(dVC/dt)]=C·[(V0·e^jω)/(d(V0·e^jω)/dt)=-jωC(2.50)

显而易见，对于理想电感和电容，其阻抗和频率相关。

注意，这里讨论的是理想电感和电容。对于非理想器件，其阻抗表达式没有这个简单，需要建立等效模型来研究，这里就不再详细讲解。

2.5.2 为什么要考虑阻抗？

是的，为什么要考虑阻抗？

在很多电子工程师的概念中，设计一个电子系统，我们更应该注重原理，只要原理设计正确，那么在系统实现的时候就不会有多大问题。没错，任何一个系统的设计过程中，如果原理出了问题，是不可挽救的，但原理的正确性只是一个系统正确工作的最基本的要求，在高速系统中，只关心这个远远不够的。

在高速系统中，随着系统时序的要求越来越严格，我们关心的不仅仅是信号连接的正确性问题，更要关心在某个时刻，某个电气连接上电压和电流的瞬时关系，这些电压和电流决定了高速系统中的所有性能。而传输线上的电压、电流的瞬时关系完全取决于传输线本身的阻抗特性。可以说，在高速系统中，所有的工作特性都取决于组成系统各部分的阻抗特性。换句话说，在高速系统中，所有的现象都可以用阻抗特性来解释。

• 由于传输线的阻抗不连续，引起信号的反射，从而引起信号本身的畸变；

• 由于传输线的耦合（耦合是阻抗构成的一部分），引起信号间的串扰，造成临近区域信号的畸变；

• 由于电源系统的某个区域分布阻抗过大，使得该区电源系统的供电不足、谐振，从而造成相关器件的性能损失，甚至混乱；

• 由以上各种阻抗特性的不可控而带来的高速信号畸变或者电源系统混乱，最后都会影响到系统的EMI（电磁干扰）。

因此，阻抗控制是高速系统设计的根本，对于高速信号系统的设计最后都会归于对信号传输阻抗的设计。在以下的章节中，我们会从各个方面来讲解如何认识阻抗，以及如何在高速系统中设计所需的传输阻抗。

2.5.3 传输线结构和传输线阻抗

对于高速电路来讲，当我们讨论传输线时，我们不仅要考虑由于高速信号而引入的新的频率因素，还要考虑由于高速信号传输而形成的不同的电路结构。理论上讲，传输线是由传输信号的信号线，即图中的微带线A，和该信号构成参考回流路径构成的。这种结构，是由传输线上的信号特征决定的，再次强调，我们讨论的不是导线上直流稳态的静电场分析，我们面临的问题是在高速信号传输过程中瞬时电磁场的交替建立过程。

所以，请特别注意，能够为信号线提供回流路径的不仅仅是通常意义的地平面，任何能够和信号线之间建立电场和磁场联系的导体，都能够和信号线之间建立传输线。而我们研究的对象是具有这些传输线结构中，能够最有效提供回流路径的那对传输线结构。正如图2-16中所示的那样，对于高速信号的传输线，其能量的传播是依靠电磁场在传输介质上的交替变化完成的，那么它的传输路径包含了：微带线本身、回流路径，以及微带线和回流路径之间的介质。所以，对于一个特定的传输线而言，信号线和回流路径之间构成的是一个双端口网络，而其阻抗，即是构成等效电路的各个因素的综合结果。

当理解了这样的信号传输结构之后，就不难立即分辨传输线阻抗和电阻的区别了。当谈到传输线的阻抗时，是绝对不能用导体A的电阻来代替的，它实质是在该传输介质中某一点上所建立的电场及流经该点的电流之间的关系，而这个“建立的电场”就是特指在显而易见的传输线和参考回路之间，所构成的传输介质上的电场。因此谈到传输线的阻抗，读者一定要建立起“两个导体”的结构概念，而不仅仅是那个显而易见的微带线A。缺少了参考回流路径，单一的微带线A是无法建立电场的。

2.5.4 瞬时阻抗和特征阻抗

当信号在传输线上传输时，每向前传输一个等效电路（这里，我们把等效电路看做信号传输方向上的最小物理单元，Δx长度的等效电路）时，都要在所经过的路径上建立相应的电磁场，并具有一定的电流经等效电路。

这时，依据前面一节中的阻抗定义，由最小传输单元的等效电路所构成的阻抗，相对于传输信号来讲，就是此时刻的瞬时阻抗。按照这个理解，信号不停地向前传播，那么对于每个时刻，信号传输到传输线的某个特定单元位置，由这个位置上的等效电路所构成的阻抗，就是该信号此时的瞬时阻抗。所以，瞬时阻抗和信号传输的时刻相关，也和该传输线的位置相关。

有一种理想的情况，如果每个时刻，该传输线上每个最小传输单元的等效电路，其物理特性都完全一致。而该信号在此传输线上传输时，每个瞬时阻抗都完全一致，那么我们就将瞬时阻抗定义为该传输线的特征阻抗。这也就从另外一个方面解释了为什么所有有关电磁理论的知识中会提到，对于特征阻抗的传输介质要求是“连续并且均匀的传输介质”了。

2.5.5 特征阻抗和信号完整性

传输线阻抗（包括瞬时阻抗和特征阻抗）是影响信号传输质量的一个重要因素。从信号传输的角度看，如果每个相邻的最小传输单元等效电路的传输阻抗完全一致，信号会被完好传输。如果相邻传输单元的阻抗不一致，那么信号的能量会被反射，这样当信号到达接收端时就会失真。对于高速系统设计，为保证良好的信号传输质量，其设计目标就是设计一个阻抗连续一致的互连系统，使得信号在整个传输路径上按照一致的特性进行传输。

可以说，在高速系统设计中，所采取的一切技巧和方法，包括减小Sub长度，进行源端或终端的匹配、采用Daisy-Chain的布线拓扑结构等，其最终目的都是要保持一个瞬时阻抗一致的传输系统，从而保证良好的信号完整性。

2.5.6 为什么是50Ω

在我们设计的系统中，几乎要求的都是50Ω的传输线阻抗。有些工程师经常会问为什么要选50Ω作为标准。其原因主要有以下几个方面。

1. 在早期的一些电子仪器中，比如雷达和电报设备，已经设计成要求信号传输阻抗为50Ω。并且，很多的电子系统测试仪也已经按照这个接口要求设计。因此延续历史习惯，现代的电子设备也要求按照50Ω的传输阻抗设计。

2. 50Ω的传输阻抗设计，有利于按照目前工艺技术和设备参数进行大规模生产。

3. 目前比较流行的CMOS器件，其输出阻抗一般在几十Ω左右，因此可以方便地和这些大规模集成电路进行互连。

4. 使用50Ω的传输阻抗设计，是对功耗、串扰、匹配、信号延迟、负载电容，以及系统集成度等几个方面综合权衡的考虑，有利于整个系统的性能优化。

如图2-17所示，是IBM研究机构给出的一个调查统计，在目前的材料和工艺水平条件下，板级系统设计中，40Ω～80Ω的设计区间是一个比较优化的选择。

图2-17 来自“Electrical Design of a High Speed Computer Package”，Evan Davidson，IBM J.of R&D，vol 26(3)May 1982，p.349。

2.6 阻抗的测量

通过上面的分析知道，将信号源连接到一段均匀的传输线上之后，从信号传输的角度，应该可以看到某一条传输线特征阻抗值，比如说是50Ω。在高速系统设计的环境中，如果某个工程师还坚持说，某条导线的阻抗值应该是零（短路）或者无穷大（开路），这种理解显然是不合适的。因为这种观点还是建立在直流稳态，以最朴素、最直观的观点来看待我们的电路，认为导线从一端到另外一端，就应该零电阻；或者认为电路另外一端开路，电阻就是无穷大。这种观点不是从高速信号传输线的角度和从传输线的物理结构上来看待问题的，这两种测量的拓扑结构的不同可以从图2-18中看到区别。

从起点到终点；另一个是“回”时间，信号被终点反射，又传回到起点的时间。

在这段时间内，测量结果是均匀传输介质，也就是电缆的特征阻抗。

• 第二时间段

起点观察到被终点反射回来的信号，新的入射信号和源源不断地被反射回来的信号叠加在一起，作为信号源来讲，所观察到的阻抗非常不稳定，始终处于一个变化的过程中，此时的测量结果，就是入射阻抗，因为入射波和反射波在传输介质中叠加成了行驻波。

• 第三时间段

当经过足够长的时间后，信号源进入直流测量状态，入射信号不再发生变化，反射信号在传输介质中消耗殆尽，这时测量结果是一个开路的直流导体，阻抗无穷大。

举例来讲，如果图2-18中的电缆只有3英寸（大约7.5cm）长，那么我们需要在大约1ns的时间间隔内完成阻抗的测量过程，这就是时域反射计（TDR）要完成的工作。TDR可以在很短的时间内测量传输线的动态阻抗。如果花1s的时间长度来测量3英尺长的线缆阻抗（包括瞬时阻抗和特征阻抗），那么在这一段时间内信号已经来回反射了几百万次，而阻抗的这些变化是在非常短的时间内完成的，1秒钟以后，由于线缆的终端是开路，那么最终得到的测量结果是无穷大，而且这个无穷大也是直流电阻，不能作为该电缆的电磁波传输阻抗。

2.7“阻抗”的困惑之答案

通过以上对阻抗的几个基本概念的讲解，回过头来我们再来看在2.5节中关于“阻抗”的困惑问题，相信部分读者已经有了答案。事实上，对于2.5节中关于微带线A阻抗的争论应该说都有一定的道理，问题是从哪个角度，如何看待这个问题。我们对这三类答案一一加以分析。

1. 微带线A的阻抗为零，因为它是一段铜线，可以认为为零

持有这种观点的读者，是把导线A当做一个导体。混淆了导体A一端到另一端的直流电阻和我们这里所说的阻抗概念。导体A的直流电阻确实应该为零，但它不是我们现在所要研究的对象。

2. 微带线A的阻抗为无穷大，因为它的末端开路

持有这种观点的读者，比第一种观点的读者更近了一步，是把导线A及相关的参考回流路径当做传输线结构来看待，这个是对的。但是，这类读者忘记了，作为传输线的阻抗，它应该具有瞬时的时间意义，是信号在传输线中高速行进过程中所遇到的物理特性。当信号到达传输线A的末端，并已经建立起稳态过程后，就失去了阻抗的瞬时意义。如果据此就认为传输线A的阻抗是“开路，无穷大”，当然是不对的。

3. 微带线A的阻抗应该为Z0，正如公式(2.23)所表示的那样

最后认为微带线A的阻抗应该为\(Z_0\)的读者，也未必完全了解了其中的含义。我们说的阻抗，应该是指微带线A的瞬时阻抗。而只有当微带线A是均匀连续的介质时，才能把微带线A的瞬时阻抗当做特征阻抗，简称阻抗。所以，在高速信号系统中，要时刻注意，我们关注的都是瞬时阻抗，只有在特定的条件下，才关心整个传输网络的（特征）阻抗，而绝不是电阻。

2.8 小结

在这一章中，我们介绍了一些关于传输线和阻抗的基本知识。虽然，这里没有严格按照电磁波的理论对各种概念和现象进行推导和验证，但是这些概念和结论是清晰无误的。在实际的工程实践中，已经有很多的仿真工具为我们提供了成熟的算法，可以进行数值分析，但是我们要清楚地知道在工具中使用的参数所表达的物理意义，所以希望读者一定对这一章的内容充分理解和掌握。

在下一章中，我们以这些基本概念和结论为基本出发点，对由于高速信号线阻抗的特性变化而引起的各种信号完整性问题进行分析，并针对这些问题提出相应的解决方案。