TC-2024《Fuzzy Clustering guided by Spectral Rotation and Scaling》

2. 核心思想

这篇论文的核心思想是提出一种名为 FCSR (Fuzzy Clustering guided by Spectral Rotation and Scaling) 的新型模糊聚类方法。该方法旨在解决传统 Fuzzy C-Means (FCM) 聚类仅从单一欧氏几何角度表示数据，无法充分捕捉数据内在结构（特别是非凸、非线性结构）的问题。

FCSR 的关键创新在于：

• 双视角表示： 同时将谱嵌入 (Spectral Embeddings, F) 和 模糊隶属度矩阵 (Membership Degrees, U) 视为数据的新表示。
• 交互引导： 在优化过程中，让这两种表示相互引导和补充。具体来说，通过谱旋转 (Spectral Rotation, R) 和谱缩放 (Spectral Scaling, $\Lambda$) 操作来调整谱嵌入 $F$，使其在某种意义上（由 Frobenius 范数衡量）更接近隶属度矩阵 $U$。
• 结构融合： 这种引导机制使得优化得到的隶属度 $U$ 不仅保留了 FCM 检测欧氏几何结构的能力，还能继承谱嵌入 $F$（基于邻接图）所揭示的数据局部邻域结构。最终目标是获得能够同时反映全局和局部数据结构的更优聚类结果。

3. 目标函数

FCSR 的目标函数如下：

$$J_{FCSR}(U,V,R,\Lambda )=\underset{U,V,R,\Lambda }{\min }\sum _{i=1}^n\sum _{k=1}^c\Vert x_i-v_k{\Vert }_2^2{u}_{ik}^2+\lambda \Vert U-\Lambda FR{\Vert }_F^2$$

约束条件为：

• $U\ge 0$ (隶属度非负)
• $U1=1$ (隶属度归一化，每行和为1)
• $R^{T}R=I$ (旋转矩阵正交)
• $\Lambda =\text{diag}([{\lambda }_{11},{\lambda }_{22},...,{\lambda }_{nn}{]}^T)$ (缩放矩阵为对角阵)
• ${\lambda }_{ii}\ge 0$ (对角元素非负)

解释：

• 第一项： ${\sum }_{i=1}^n{\sum }_{k=1}^c\Vert x_i-v_k{\Vert }_2^2{u}_{ik}^2$ 是标准 FCM 目标函数的一部分（模糊系数 $m$ 固定为2），用于最小化数据点到其聚类中心的加权平方距离，侧重于捕捉全局欧氏结构。
• 第二项： $\lambda \Vert U-\Lambda FR{\Vert }_F^2$ 是 FCSR 的核心创新项。它通过 Frobenius 范数衡量隶属度矩阵 $U$ 与经过旋转 $R$ 和缩放 $\Lambda$ 变换后的谱嵌入矩阵 $F$ 之间的差异。$\lambda$ 是平衡两项贡献的参数。
• 目标： 通过最小化整个目标函数，使得聚类结果（由 $U$ 和 $V$ 表示）既能符合传统的欧氏距离准则，又能受到谱嵌入所蕴含的邻域结构信息的引导。

4. 目标函数详细的优化过程

论文采用交替优化 (Alternative Optimization) 策略，每次固定其他变量，优化一个变量。

• 优化 $U$ (当 $V,R,\Lambda$ 固定时):

  • 令 $Q=\Lambda FR$，目标函数关于 $U$ 的部分变为：$J={\sum }_{i=1}^n{\sum }_{k=1}^c[\Vert x_i-v_k{\Vert }_2^2{u}_{ik}^2+\lambda (u_{ik}-q_{ik}{)}^2]$。
  • 对每个样本 $i$，优化问题简化为：${\min }_{u_{i\cdot }}\Vert u_{i\cdot }-h_{i\cdot }{\Vert }_2^2$，其中 $h_{ik}=\frac{\lambda q_{ik}}{d_{ik}^2+\lambda }$，$d_{ik}=\Vert x_i-v_k{\Vert }_2$。
  • 约束条件为 $u_{i\cdot }\ge 0$ 且 $u_{i\cdot }1=1$。这是一个带约束的二次优化问题，可以通过特定的优化技巧（如论文引用的[34]）求解。

• 优化 $V$ (当 $U,R,\Lambda$ 固定时):

  • 对目标函数关于 $v_k$ 求导并令其为零：$\frac{\partial J_{FCSR}}{\partial v_k}=0$。
  • 解得：$v_k=\frac{{\sum }_{i=1}^n{x}_i{u}_{ik}^2}{{\sum }_{i=1}^n{u}_{ik}^2}$。这与标准 FCM 更新聚类中心的公式一致。

• 优化 $R$ (当 $U,V,\Lambda$ 固定时):

  • 问题简化为：${\min }_R\Vert U-\Lambda FR{\Vert }_F^2$，约束 $R^{T}R=I$。这是一个经典的正交 Procrustes 问题 (Orthogonal Procrustes Problem)。
  • 通过展开范数并利用迹的性质，等价于最大化 $\text{tr}(R^T{F}^T\Lambda U)$。
  • 令 $M=F^T\Lambda U$，对其进行奇异值分解 (SVD)：$M=A\Sigma B^T$。
  • 最优解为：$R=A{B}^T$。

• 优化 $\Lambda$ (当 $U,V,R$ 固定时):

  • 令 $\Psi =FR$，问题简化为：${\min }_{\Lambda }\Vert U-\Lambda \Psi {\Vert }_F^2={\sum }_{i=1}^n\Vert u_{i\cdot }-{\lambda }_{ii}{\psi }_{i\cdot }{\Vert }_2^2$。
  • 对每个对角元素 ${\lambda }_{ii}$ 独立优化：${\lambda }_{ii}={\left[\frac{u_{i\cdot }{\psi }_{i\cdot }^T}{{\psi }_{i\cdot }{\psi }_{i\cdot }^T}\right]}_{+}$，其中 $[a{]}_{+}=\max (a,0)$。如果 $F$ 已行归一化，则简化为 ${\lambda }_{ii}=[u_{i\cdot }{\psi }_{i\cdot }^T{]}_{+}$。

5. 主要贡献点

1. 提出新颖的 FCSR 模型： 首次将谱嵌入和模糊隶属度视为数据的两种互补表示，并通过谱旋转和缩放操作将它们在优化过程中进行对齐和引导，从而融合了 FCM 和 SC 的优势。
2. 增强数据结构捕捉能力： 通过引入谱信息引导，使得 FCSR 能够处理任意形状（特别是非凸）的数据，克服了传统 FCM 的局限性。
3. 提出 FCSR-P 和 FCSR-K 变体： 为了提高模型的适应性和扩展性，分别提出了适用于高维数据的投影版本 (FCSR-P) 和能改善线性可分性的核版本 (FCSR-K)。
4. 理论与实验验证： 论文从理论上分析了优化过程的收敛性，并通过在多个知名数据集上的大量实验证明了所提方法（FCSR, FCSR-P, FCSR-K）的有效性，显著优于多种代表性模糊聚类方法。

6. 算法实现过程 (以 FCSR 为例)

FCSR 算法的具体步骤如下（对应论文 Algorithm 1）：

• 输入： 数据集 $X$，平衡参数 $\lambda$，预计算的谱嵌入 $F$。
• 输出： 聚类中心 $V$，最终隶属度矩阵 $U$。
• 初始化： 在约束 $U1=1$ 和 $U\ge 0$ 下初始化 $U$；初始化缩放矩阵 $\Lambda =I$（单位矩阵）。
• 迭代优化：
  1. 更新 $V$： 使用公式 $v_k=\frac{{\sum }_{i=1}^n{x}_i{u}_{ik}^2}{{\sum }_{i=1}^n{u}_{ik}^2}$ 更新所有聚类中心。
  2. 更新 $R$： 计算 $M=F^T\Lambda U$，对 $M$ 进行 SVD 得到 $M=A\Sigma B^T$，更新旋转矩阵 $R=A{B}^T$。
  3. 更新 $\Lambda$： 计算 $\Psi =FR$，使用公式 ${\lambda }_{ii}=[u_{i\cdot }{\psi }_{i\cdot }^T{]}_{+}$ 更新对角矩阵 $\Lambda$ 的对角元素。
  4. 更新 $U$： 计算辅助矩阵 $H$（元素 $h_{ik}=\frac{\lambda (\Lambda FR{)}_{ik}}{d_{ik}^2+\lambda }$），在约束 $u_{i\cdot }\ge 0$ 且 $u_{i\cdot }1=1$ 下，求解 ${\min }_{u_{i\cdot }}\Vert u_{i\cdot }-h_{i\cdot }{\Vert }_2^2$ 得到新的 $u_{i\cdot }$。
• 循环： 重复步骤 1-4，直到算法收敛（例如，目标函数值变化小于阈值或达到最大迭代次数）。
• 获取最终聚类结果： 算法收敛后，得到最终的隶属度矩阵 $U$。对于每个样本 $x_i$，将其分配给隶属度最大的类别 $k$（即 $\arg {\max }_k{u}_{ik}$）。

总结: FCSR 通过巧妙地结合 FCM 和 SC 的思想，利用谱旋转和缩放操作引导隶属度矩阵的优化，旨在获得更准确、更能反映数据内在结构的聚类结果。其变体 FCSR-P 和 FCSR-K 进一步拓展了其应用范围。

这段文字是论文中对目标函数 (6) 的核心思想进行的深入解释，它清晰地阐述了 FCSR 方法为何以及如何超越传统的 FCM。我们可以从以下几个层面来理解：

1. 目标函数的两个组成部分

目标函数 $J_{FCSR}$ 包含两个关键项：

• 第一项： ${\sum }_{i=1}^n{\sum }_{k=1}^c\Vert x_i-v_k{\Vert }_2^2{u}_{ik}^2$。这与标准 FCM 的目标函数完全相同（模糊系数 $m$ 固定为 2）。它的作用是最小化数据点到聚类中心的加权平方距离，这使得模型能够捕捉数据的全局欧氏几何结构（例如，球形或椭球形簇）。
• 第二项： $\lambda \Vert U-\Lambda FR{\Vert }_F^2$。这是 FCSR 的创新之处。它引入了一个新的约束，旨在让隶属度矩阵 $U$ 尽可能接近一个经过变换的谱嵌入矩阵 $F$。

2. 谱嵌入 $F$ 和旋转/缩放矩阵 $R$, $\Lambda$

• 谱嵌入 $F$: 这个矩阵是通过求解谱聚类 (SC) 的问题 (4) 得到的，即对拉普拉斯矩阵进行特征值分解，并取前 $c$ 个最小特征值对应的特征向量构成。$F$ 可以看作是原始数据在低维“谱空间”中的新表示。这个表示的核心优势在于，它保留了数据的局部邻域结构（manifold structure），因此能够有效地处理任意形状的非凸数据集。
• 旋转矩阵 $R$: 由于 $U$ 和 $F$ 分别属于不同的数学空间（$U$ 是一个受简单形约束的矩阵，而 $F$ 是一个连续的、无特定约束的矩阵），它们的坐标轴方向和尺度可能不一致。$R$ 是一个正交矩阵，其作用是旋转 $F$ 空间，使其坐标轴与 $U$ 空间的坐标轴对齐，从而减少两个空间之间的偏移。
• 缩放矩阵 $\Lambda$: 即使经过旋转，$U$ 和 $F$ 中每个样本向量的长度（范数）也可能不同。例如，$U$ 中的行向量 $u_i$ 满足 $0<\Vert u_i{\Vert }_2\le 1$，而 $F$ 中的行向量 $f_i$ 通常被归一化为单位长度 ($\Vert f_i{\Vert }_2=1$)。$\Lambda$ 是一个对角矩阵，其对角线元素 ${\lambda }_{ii}\ge 0$，用于缩放 $F$ 空间中每个样本向量的长度，使其与 $U$ 空间中对应向量的长度相匹配。

3. 为什么需要 $R$ 和 $\Lambda$？——空间对齐与偏差缓解

作者强调，FCSR 并不是简单地将 FCM 和 SC 的结果“拼接”在一起。而是创造了一种可行的机制，用来实现不同表示空间之间的对齐。具体来说：

• 解决范数差异： $U$ 和 $F$ 的范数不同，直接比较会失真。$\Lambda$ 通过缩放操作解决了这个问题。
• 解决坐标系偏差： $U$ 和 $F$ 的坐标系可能不一致。$R$ 通过旋转操作，将 $F$ 的坐标系“旋转”到与 $U$ 的坐标系对齐的位置。

通过同时应用旋转和缩放操作，FCSR 成功地对齐了两种表示空间，并缓解了它们之间的固有偏差。

4. 互补性与最终效果

• 互补性： $U$ 捕获的是数据的全局几何结构（global geometrical structure），而 $F$ 捕获的是数据的局部流形特性（local manifold properties）。两者从不同的视角描述了相同的数据，因此可以相互补充。
• 引导与继承： 在 FCSR 中，优化过程是在 $F$ 的“引导”下进行的。这意味着，传统 FCM 所得到的隶属度 $U$ 会发生变化，并继承了谱嵌入 $F$ 的优点。最终得到的 $U$ 不再仅仅是基于欧氏距离的，而是融合了局部邻域信息。
• 提升性能： 因此，FCSR 所获得的隶属度 $U$ 更适合于检测非椭球形（nonellipsoidal）的数据结构，因为它结合了 FCM 对全局结构的敏感性和 SC 对局部结构的强大捕捉能力。

总结来说，这段话的核心思想是： FCSR 通过引入旋转和缩放操作，巧妙地将谱聚类（SC）揭示的局部结构信息，作为“引导”融入到传统的模糊 C-均值（FCM）聚类过程中。它不是简单地组合两种方法，而是通过空间对齐，让两种互补的数据表示（全局几何 vs 局部流形）协同工作，从而生成一个更强大、更能反映数据真实内在结构的聚类结果。

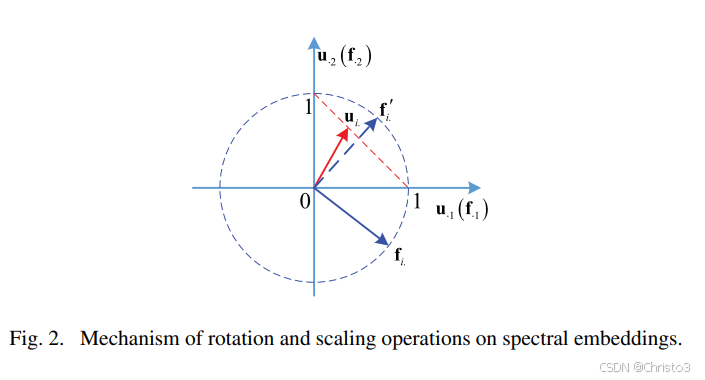
这段文字通过一个具体的例子（聚类数 $c=2$）来直观地解释 FCSR 模型中旋转 (Rotation) 和 缩放 (Scaling) 操作的核心作用。我们可以将其分解为以下几个关键点来理解：

1. 理解隶属度向量 $ \mathbf{u}_i $ 的几何约束

• 约束条件： 在 FCM 中，每个样本的隶属度向量 $ \mathbf{u}i = [u{i1}, u_{i2}] $ 必须满足两个约束：
  1. 非负性 (Non-negativity): $ u_{i1} \geq 0, u_{i2} \geq 0 $
  2. 归一化 (Normalization): $ u_{i1} + u_{i2} = 1 $
• 几何表示： 这两个约束将所有可能的隶属度向量 $ \mathbf{u}_i $ 限制在二维平面上的一个特定区域内——即第一象限中的线段 $ u_1 + u_2 = 1 $ 上（如图2中的红色虚线所示）。这意味着，无论数据如何，FCM 得到的隶属度都只能在这条线上移动。

2. 理解谱嵌入向量 $ \mathbf{f}_i $ 的几何特性

• 无约束性： 谱嵌入 $ \mathbf{f}_i $ 是通过求解拉普拉斯矩阵的特征值问题得到的。它是一个连续的、无特定约束的向量。
• 自由分布： 因此，$ \mathbf{f}_i $ 可以出现在二维平面的任何位置，即可以位于四个象限中的任何一个。这反映了谱嵌入能够捕捉数据的复杂局部结构（例如，非凸形状），而这种结构可能无法用简单的欧氏距离或一个固定维度的线段来描述。

3. 旋转 (Rotation) 操作的作用

• 目的： 旋转操作 $ \mathbf{f}_i’ = \mathbf{f}_i \mathbf{R} $ 的目的是将谱嵌入向量 $ \mathbf{f}_i $ 从其原始位置“移动”到与隶属度向量 $ \mathbf{u}_i $ 所在空间（第一象限的线段）更接近的位置。
• 具体操作： 由于 $ \mathbf{u}_i $ 被限制在第一象限，而 $ \mathbf{f}_i $ 可能在其他象限，旋转操作 $ \mathbf{R} $ 就像一个坐标系的变换，它会将整个谱嵌入空间进行旋转，使得原本在第二、第三或第四象限的 $ \mathbf{f}_i $ 向量被“转”到第一象限。
• 效果： 经过旋转后，$ \mathbf{f}_i’ $ 位于第一象限，这就消除了 $ \mathbf{u}_i $ 和 $ \mathbf{f}_i $ 之间因坐标轴方向不同而导致的“偏移”（bias）。

4. 缩放 (Scaling) 操作的作用

• 目的： 即使经过旋转，$ \mathbf{f}_i’ $ 和 $ \mathbf{u}_i $ 的长度（范数）也可能不同。例如，$ \mathbf{u}_i $ 的长度是 $ |\mathbf{u}i|2 = \sqrt{u{i1}^2 + u{i2}^2} \leq 1 $，而 $ \mathbf{f}_i’ $ 的长度可能是任意正数。缩放操作 $ \Lambda_i \mathbf{f}_i’ $ 的目的是调整 $ \mathbf{f}_i’ $ 的大小，使其长度与 $ \mathbf{u}_i $ 更匹配。
• 具体操作： 对于每个样本 $ i $，使用一个单独的缩放因子 $ \Lambda_i $（对角矩阵 $ \Lambda $ 的对角元素）来乘以旋转后的向量 $ \mathbf{f}_i’ $。
• 效果： 这样做可以“拉伸”或“压缩” $ \mathbf{f}_i’ $，从而弥补了两种表示空间在尺度上的差异。

5. 整体过程与最终效果

1. 原始状态： $ \mathbf{u}_i $ 被严格限制在第一象限的线段上，而 $ \mathbf{f}_i $ 可以自由分布在四个象限。
2. 应用旋转： $ \mathbf{f}_i $ 被旋转到第一象限，变成 $ \mathbf{f}_i’ $。
3. 应用缩放： $ \mathbf{f}_i’ $ 被缩放，变成 $ \Lambda_i \mathbf{f}_i’ $，其长度与 $ \mathbf{u}_i $ 更接近。
4. 目标： 最终的目标是让优化得到的隶属度向量 $ \mathbf{u}_i $ 尽可能靠近这个经过旋转和缩放处理后的 $ \Lambda_i \mathbf{f}_i’ $。
5. 结果： 通过这种方式，FCSR 模型引导 $ \mathbf{u}_i $ 不再仅仅由欧氏距离决定，而是也受到谱嵌入所揭示的局部邻域结构的影响。因此，最终得到的隶属度不仅保留了 FCM 的优点，还继承了谱嵌入捕捉复杂数据结构的能力，从而更有效地识别非椭球形的数据簇。

总结来说，这段话的核心思想是： 由于隶属度向量和谱嵌入向量属于不同的数学空间（一个有约束，一个无约束），它们之间存在天然的“鸿沟”。FCSR 通过引入旋转和缩放操作，巧妙地将谱嵌入向量“翻译”成与隶属度向量同在一个“语言”（即第一象限且尺度相近）下的表达形式，从而实现了两种互补信息的有效融合。