代码随想录Day57:图论(寻宝prim算法精讲kruskal算法精讲)
一、实战
prim算法精讲
53. 寻宝(第七期模拟笔试)
最小生成树:所有节点的最小连通子图,即:以最小的成本(边的权值)将图中所有节点链接到一起。图中有n个节点,那么一定可以用n-1条边将所有节点连接到一起。
prim算法:从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。(minDist数组是prim算法的灵魂,它帮助prim算法完成最重要的一步,就是如何找到距离最小生成树最近的点。)
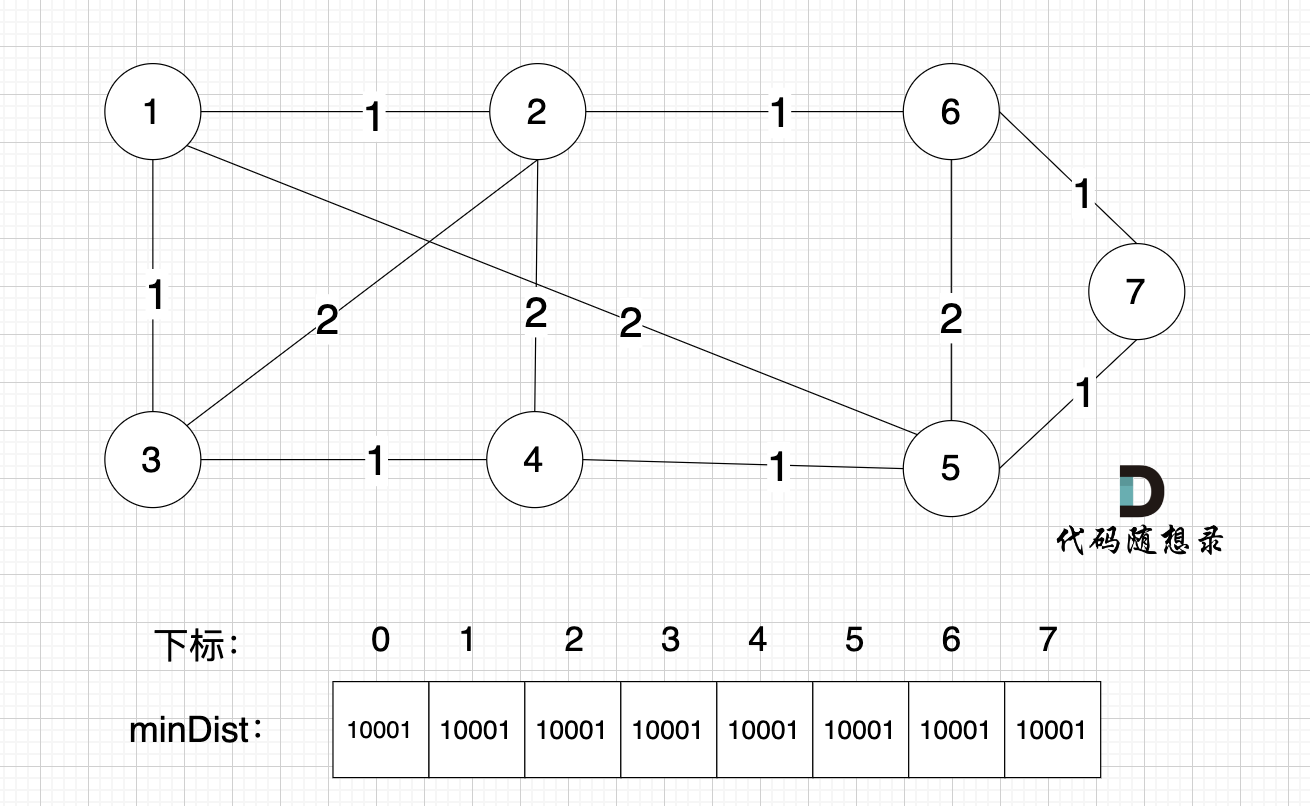
prim三部曲:
- 第一步,选距离生成树最近节点。选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那我们选择节点1
- 第二步,最近节点加入生成树。此时节点1已经算最小生成树的节点。
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组。minDist数组用来记录每一个节点距离最小生成树的最近距离。)此时所有非生成树的节点距离最小生成树(节点1)的距离都已经跟新了。
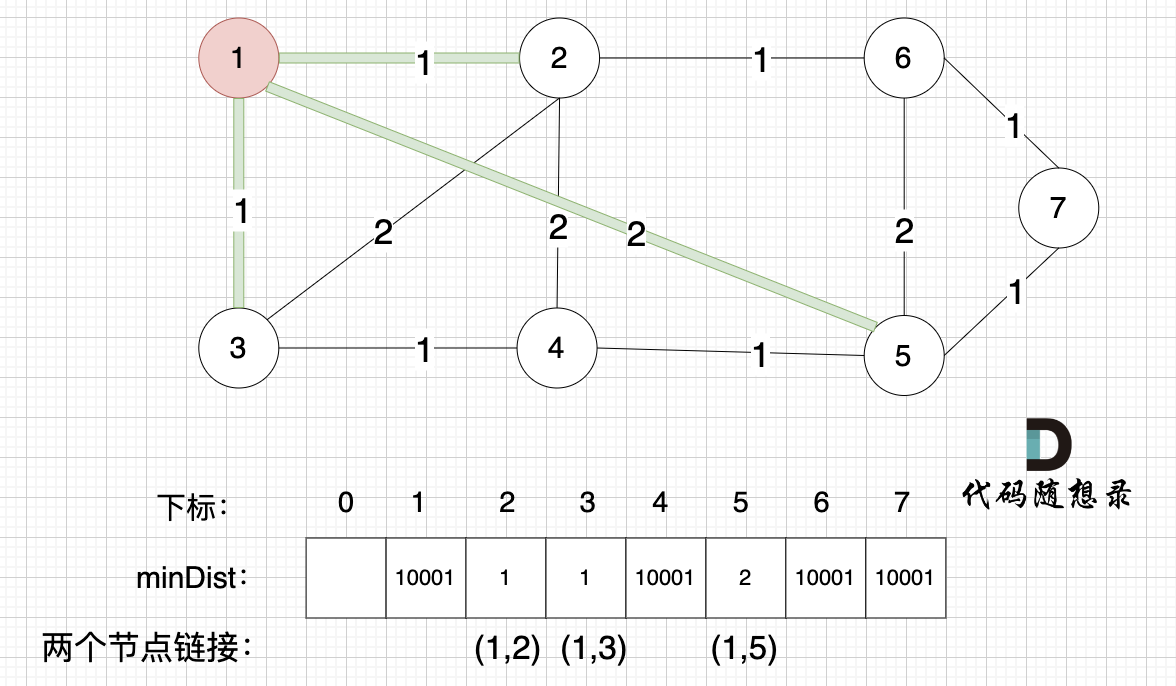
注意:下标0不用管,下标1与节点1对应,这样可以避免把节点搞混。
后面就是重复三部曲的过程。
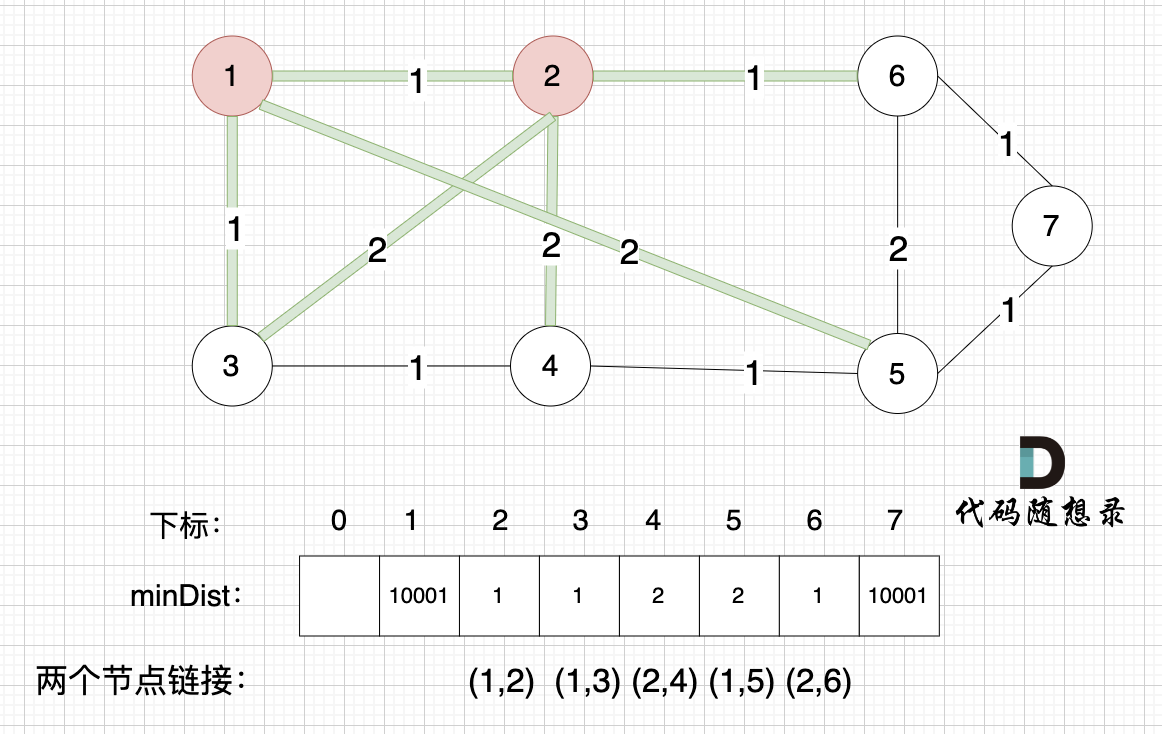
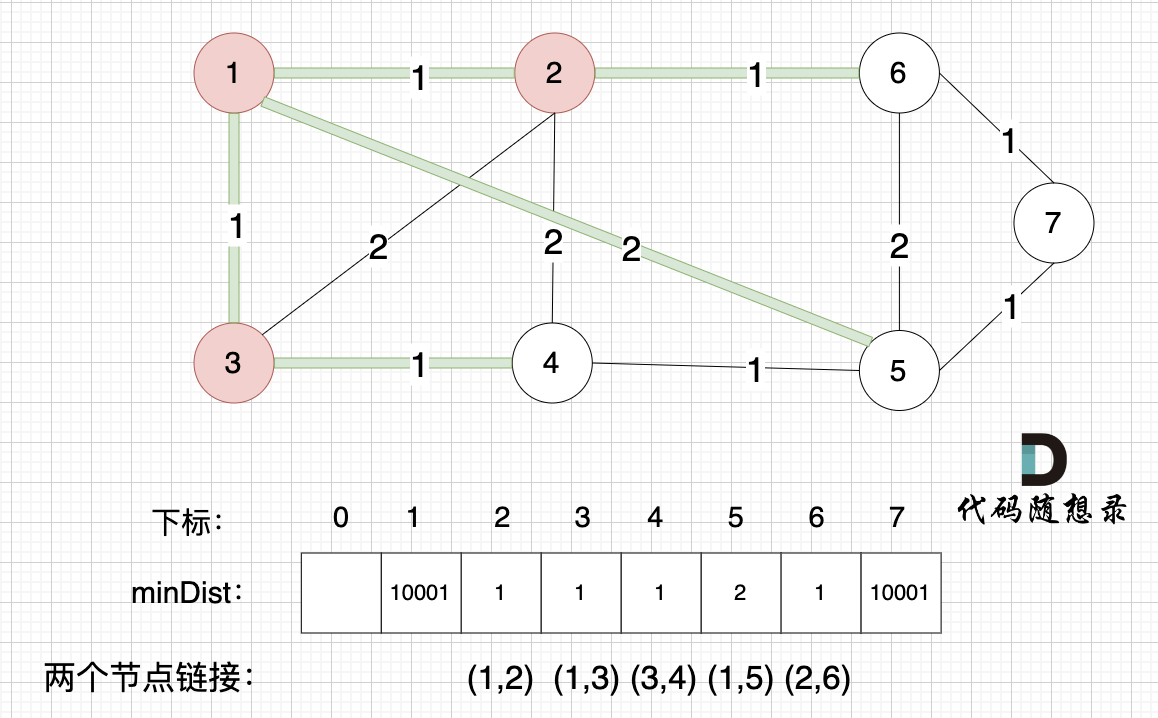
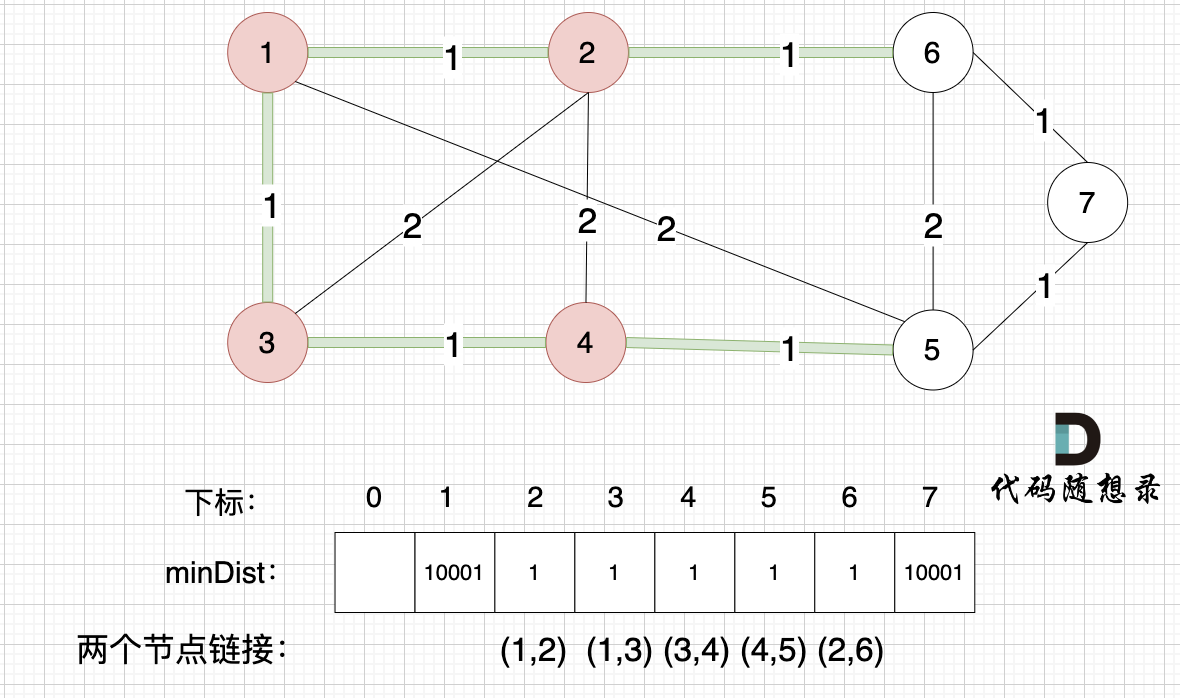
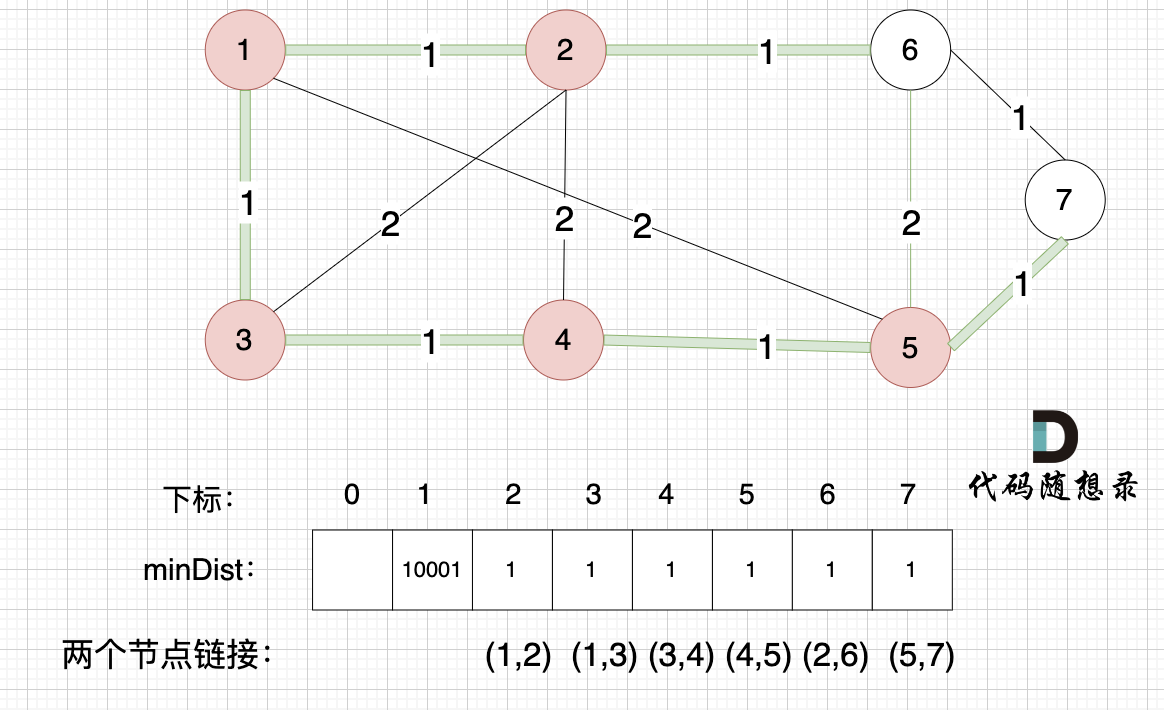
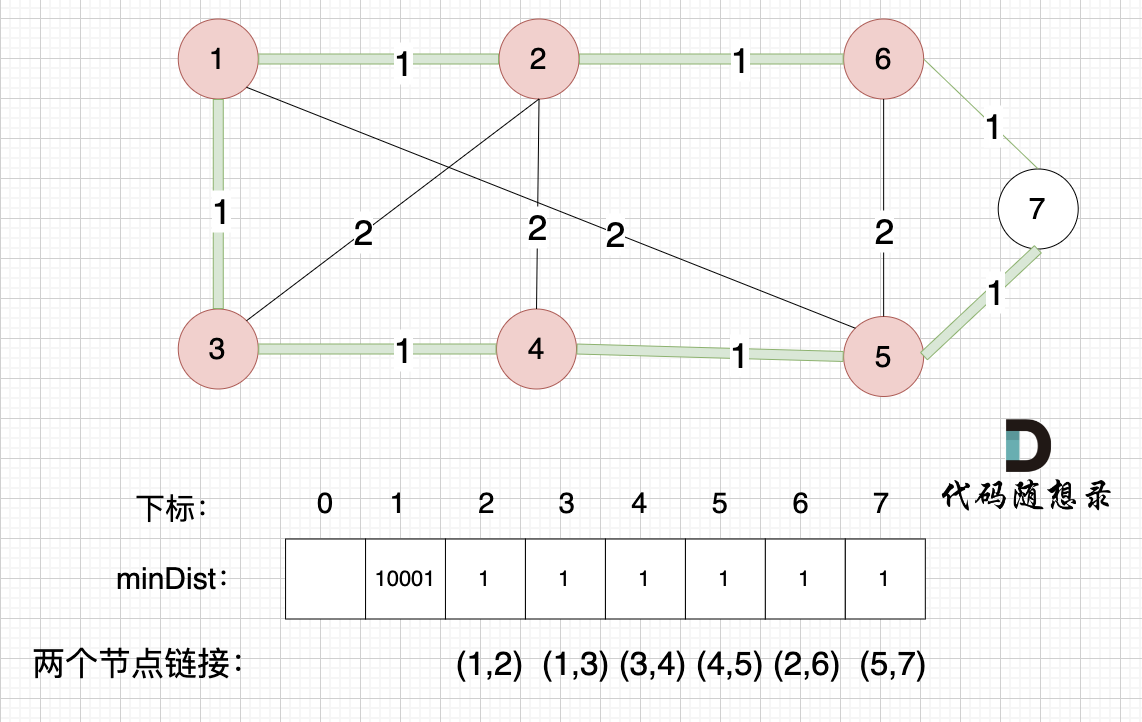
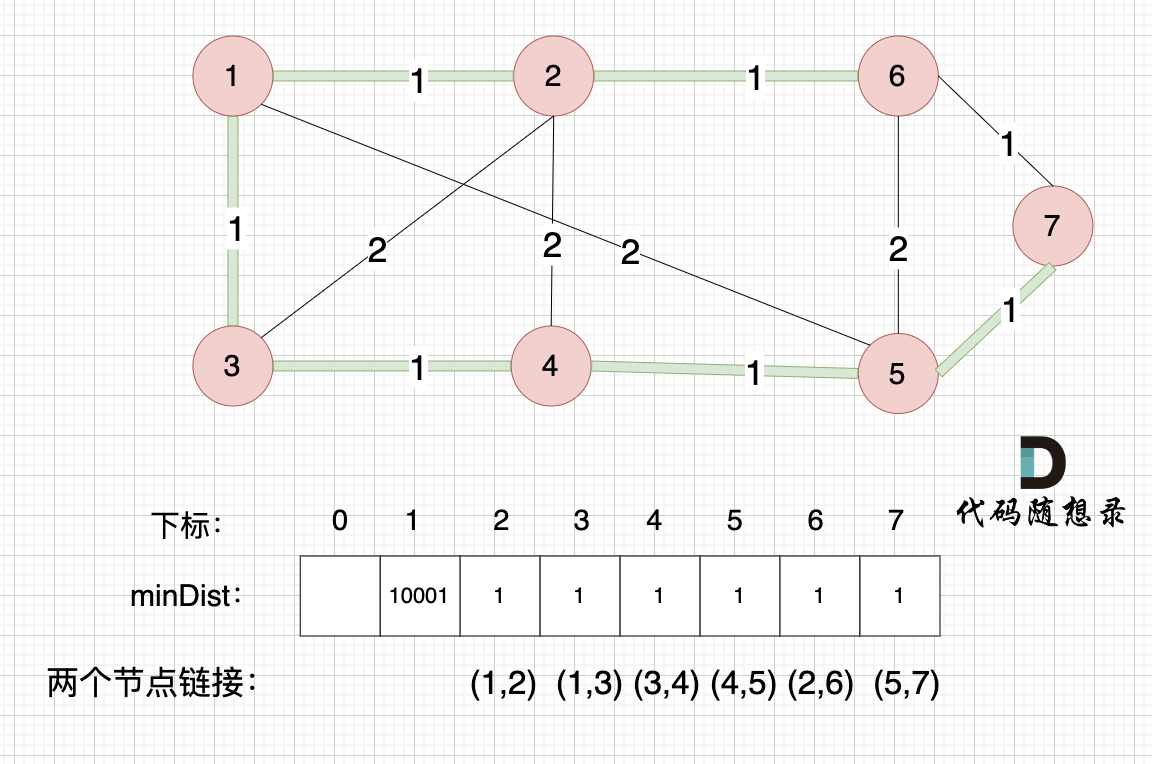
最后,minDist数组也就是记录的是最小生成树所有边的权值,要求最小生成树里边的权值总和就是把最后的minDist数组累加一起。
import java.util.*;public class Main{public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int v = scanner.nextInt(); // 读入顶点数int e = scanner.nextInt(); // 读入边数// 创建邻接矩阵,表示图中各点之间的边权int[][] grid = new int[v+1][v+1];for (int i = 0; i <= v; i++) {Arrays.fill(grid[i], Integer.MAX_VALUE); // 初始化为无穷大,表示无边}// 读入每条边,并填充邻接矩阵(无向图,双向赋值)for (int i = 0; i < e; i++) {int x = scanner.nextInt(); // 边的起点int y = scanner.nextInt(); // 边的终点int k = scanner.nextInt(); // 边的权重grid[x][y] = k; // 正向边grid[y][x] = k; // 反向边(无向图)}// minDist[i] 表示当前生成树到节点 i 的最短边权int[] minDist = new int[v+1];Arrays.fill(minDist, Integer.MAX_VALUE); // 初始化所有距离为无穷大boolean[] isInTree = new boolean[v + 1]; // 标记节点是否已加入最小生成树// Prim 算法主循环:需要加入 n-1 个节点(除起点外)for (int i = 1; i < v; i++) {int cur = 1; // 临时变量:用于记录当前要加入的节点int minValue = Integer.MAX_VALUE; // 临时变量:记录当前最小距离// 遍历所有节点,寻找未加入树中且距离最小的节点for(int j = 1; j <= v; j++) {if(!isInTree[j] && minDist[j] < minValue) {minValue = minDist[j]; // 更新最小距离cur = j; // 记录该节点}}isInTree[cur] = true; // 将找到的最近节点加入生成树// 用新加入的节点 cur 更新其他节点到生成树的最短距离for(int j = 1; j <= v; j++) {if(!isInTree[j] && grid[cur][j] < minDist[j]) {minDist[j] = grid[cur][j]; // 松弛操作:发现更短边则更新}}}// 累加最小生成树的总权重(注意从 i=2 开始,跳过0和1)int result = 0;for (int i = 2; i <= v; i++) {result += minDist[i]; // 累加每个节点连到生成树的边权}System.out.println(result); // 输出最小生成树的总权重scanner.close(); }
}kruskal算法精讲
53. 寻宝(第七期模拟笔试)
kruscal的思路:
- 边的权值排序,因为要优先选最小的边加入到生成树里
- 遍历排序后的边
- 如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环
- 如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合
将图中的边按照权值有小到大排序,这样从贪心的角度来说,优先选 权值小的边加入到 最小生成树中。排序后的边顺序为[(1,2) (4,5) (1,3) (2,6) (3,4) (6,7) (5,7) (1,5) (3,2) (2,4) (5,6)]权值相同,前后顺序任意
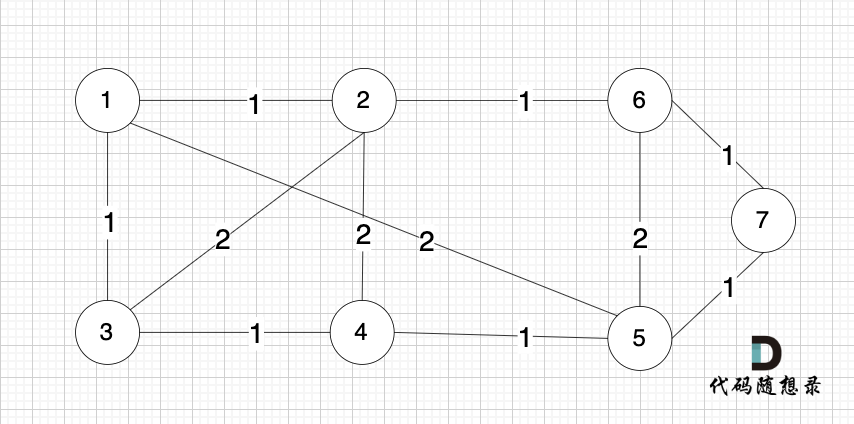
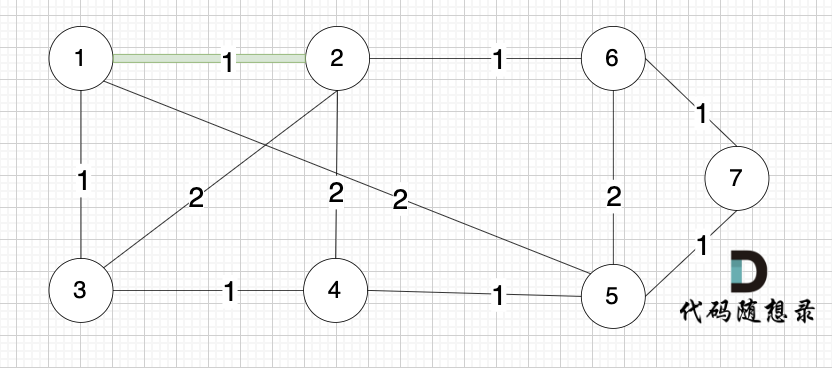
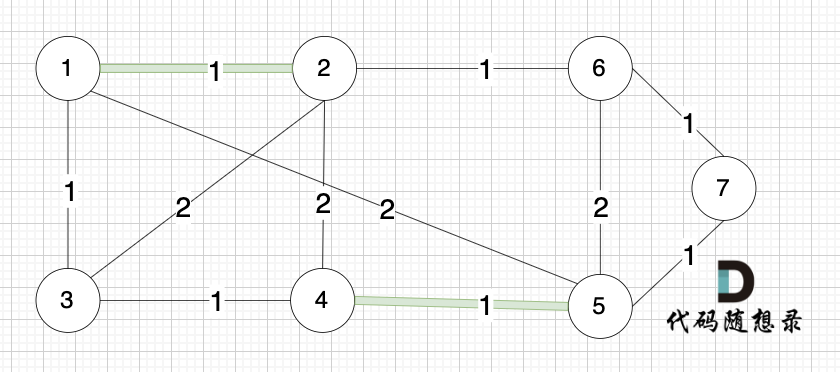
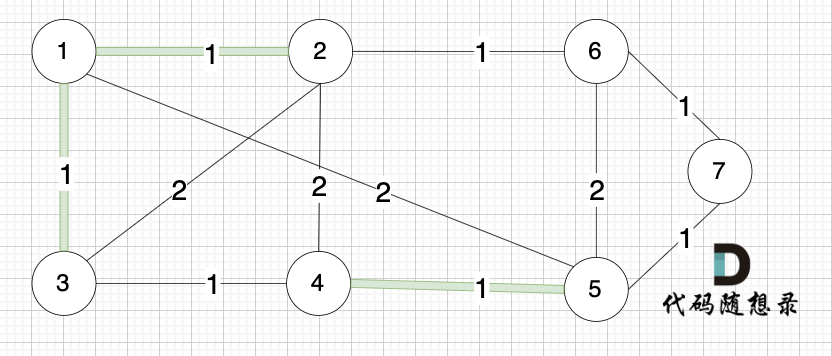
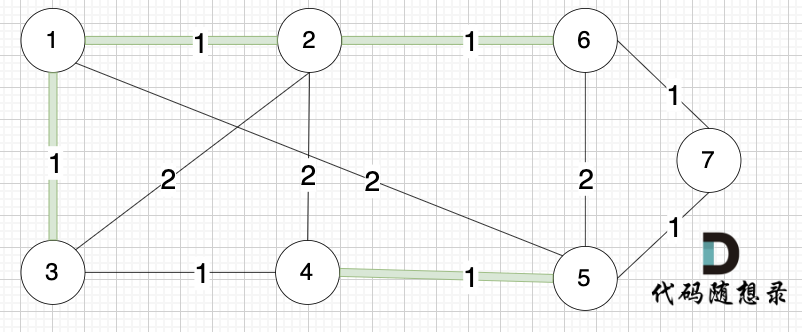
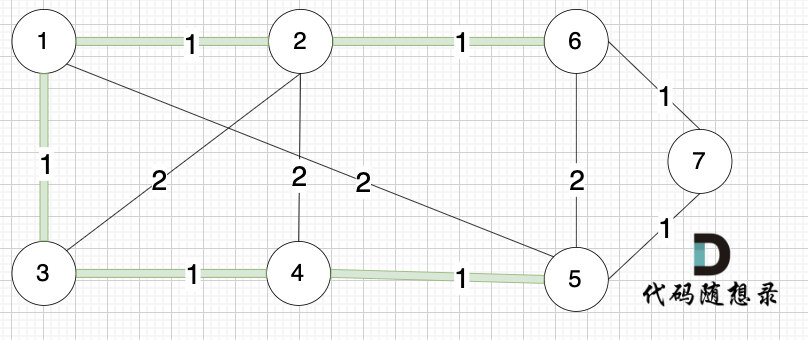
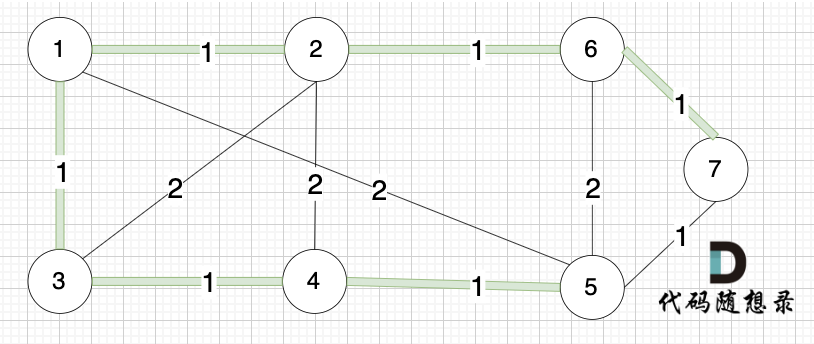
选边(5,7),节点5 和 节点7 在同一个集合,不做计算。选边(1,5),两个节点在同一个集合,不做计算。后面遍历 边(3,2),(2,4),(5,6) 同理,都因两个节点已经在同一集合,不做计算。此时 我们就已经生成了一个最小生成树如上图。
在代码中,如果将两个节点加入同一个集合,又如何判断两个节点是否在同一个集合呢?就是我们之前学习的并查集
二、两种算法的区别
Kruskal 与 prim 的关键区别在于,prim维护的是节点的集合,而 Kruskal 维护的是边的集合。 如果 一个图中,节点多,但边相对较少,那么使用Kruskal 更优。
一个图里怎么可能节点多,边却少呢?节点未必一定要连着边那, 例如 这个图,大家能明显感受到边没有那么多对吧,但节点数量 和 上述我们讲的例子是一样的。
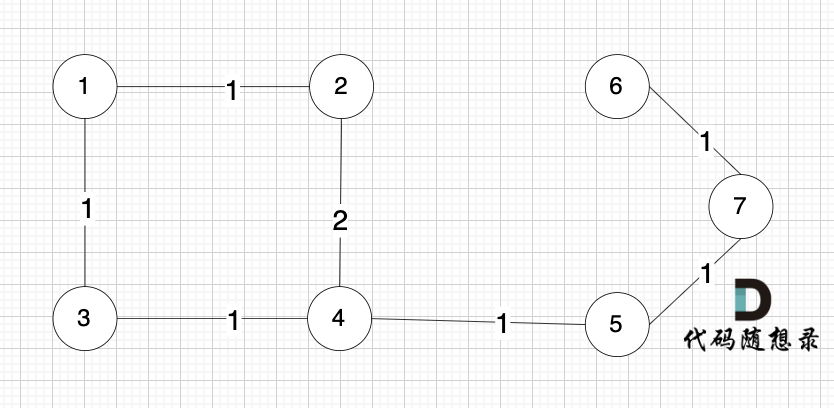
为什么边少的话,使用 Kruskal 更优呢?因为 Kruskal 是对边进行排序的后 进行操作是否加入到最小生成树。边如果少,那么遍历操作的次数就少。在节点数量固定的情况下,图中的边越少,Kruskal 需要遍历的边也就越少。而 prim 算法是对节点进行操作的,节点数量越少,prim算法效率就越优。
所以在 稀疏图中,用Kruskal更优。 在稠密图中,用prim算法更优。
边数量较少为稀疏图,接近或等于完全图(所有节点皆相连)为稠密图
Prim 算法 时间复杂度为 O(n^2),其中 n 为节点数量,它的运行效率和图中边树无关,适用稠密图。Kruskal算法 时间复杂度 为 nlogn,其中n 为边的数量,适用稀疏图。
import java.util.*;// 定义一条边:起点、终点、权重
class Edge {int from, to, weight;Edge(int from, int to, int weight) {this.from = from;this.to = to;this.weight = weight;}
}public class Main {// 并查集数组:记录每个节点的“老大”private static int[] parent = new int[10001];// 并查集初始化:每个节点自己是自己的老大public static void initUnionFind() {for (int i = 0; i < 10001; i++) {parent[i] = i;}}// 查找 x 的根节点(路径压缩优化)public static int findRoot(int x) {if (x == parent[x]) return x;return parent[x] = findRoot(parent[x]); // 路径压缩}// 合并两个集合public static void union(int x, int y) {int rootX = findRoot(x);int rootY = findRoot(y);if (rootX == rootY) return; // 已在同一集合parent[rootY] = rootX; // 把 y 的根挂到 x 的根上}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int V = scanner.nextInt(); // 顶点数int E = scanner.nextInt(); // 边数List<Edge> edges = new ArrayList<>(); // 存所有边int totalCost = 0; // 最小总距离// 读入每条边for (int i = 0; i < E; i++) {int v1 = scanner.nextInt();int v2 = scanner.nextInt();int w = scanner.nextInt();edges.add(new Edge(v1, v2, w));}// 按边的长度从小到大排序(贪心策略)edges.sort(Comparator.comparingInt(e -> e.weight));// 初始化并查集initUnionFind();// 遍历每条边(从最短的开始)for (Edge e : edges) {int root1 = findRoot(e.from);int root2 = findRoot(e.to);// 如果两个点还不连通,就加上这条边if (root1 != root2) {totalCost += e.weight; // 累加这条边的长度union(e.from, e.to); // 把这两个点连起来}// 如果已经连通了,跳过(避免成环)}System.out.println(totalCost); // 输出最小总长度scanner.close();}
}