从概率到实践：深度解析朴素贝叶斯分类算法

引言：当数学遇见数据的魔法

在机器学习的浩瀚星空中，朴素贝叶斯算法如同一颗独特的星辰，以其简洁优雅的数学原理和高效实用的工程价值闪耀着光芒。这个诞生于 18 世纪的概率理论，经过现代数据科学的洗礼，已经成为文本分类、医疗诊断、金融风控等领域的核心工具。想象一下，当你收到一封邮件，算法如何瞬间判断它是垃圾邮件还是重要通知？当医生面对复杂的检测报告，如何快速锁定潜在疾病？这些看似神奇的决策背后，都隐藏着朴素贝叶斯的智慧。

本文将带你从概率理论的基石出发，逐步揭开朴素贝叶斯的神秘面纱。我们不仅会深入探讨其数学原理，更会通过丰富的案例和代码实践，让你真正掌握这门技术的精髓。无论你是机器学习的初学者，还是希望优化现有模型的工程师，本文都将为你提供实用的见解和可复用的解决方案。

一、贝叶斯分类理论：用概率做决策的艺术

1.1 决策的核心逻辑：选择高概率路径

假设我们有一个二维数据集，其中红色圆点代表类别 1，蓝色三角形代表类别 2（如图 1 所示）。对于一个新数据点 (x, y)，我们需要判断它属于哪个类别。贝叶斯决策理论给出了一个简单而强大的规则：

如果 p₁(x,y) > p₂(x,y)，则判定为类别 1；否则判定为类别 2。

这里的 p₁和 p₂分别表示数据点属于类别 1 和类别 2 的概率。这个规则的本质是最大化后验概率，即选择概率最大的决策路径。就像在岔路口选择最可能到达目的地的道路一样，贝叶斯分类器通过概率计算为我们指明方向。

1.2 概率的本质：不确定性的量化

在机器学习中，概率不仅是数学概念，更是处理不确定性的工具。例如，在医疗诊断中，p (患病 | 症状) 表示出现某种症状时患病的概率。这种概率不是绝对的确定性，而是基于现有数据的统计推断。贝叶斯分类器的优势在于，它能够将这种不确定性转化为可操作的决策，为我们在信息不完全的情况下提供最优解。

二、条件概率：透过现象看本质

2.1 事件的依赖关系：文氏图的启示

条件概率 P (A|B) 表示在事件 B 发生的情况下，事件 A 发生的概率。通过文氏图（图 2），我们可以直观地理解这一概念：在事件 B 的范围内，事件 A 与 B 的交集部分占 B 的比例即为 P (A|B)。数学上，这可以表示为：

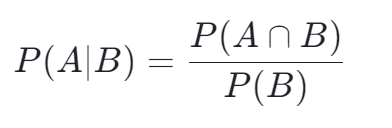
2.2 乘法法则：联合概率的分解

由条件概率公式可以推导出联合概率的计算方法：

这一公式揭示了两个事件同时发生的概率，等于其中一个事件发生的概率乘以在该事件发生条件下另一个事件发生的概率。例如，计算 “今天下雨且堵车” 的概率，可以分解为 “今天下雨的概率” 乘以 “下雨时堵车的概率”。

2.3 逆向思维：贝叶斯定理的诞生

将条件概率公式变形，我们得到了贝叶斯定理的雏形：

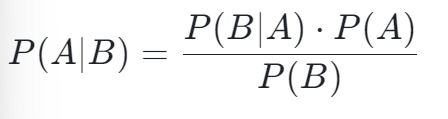
这个公式的意义在于，它允许我们通过已知的 P (B|A) 来推断 P (A|B)，即从结果反推原因的概率。例如，已知某种疾病在人群中的发病率（P (A)）、患病者出现症状的概率（P (B|A)），以及症状在人群中的总体发生率（P (B)），我们就可以计算出出现症状时患病的概率（P (A|B)）。

三、全概率公式：从局部到全局的视角

3.1 样本空间的划分：红蓝世界的启示

全概率公式是贝叶斯定理的重要基石，它描述了一个事件的概率如何由其在不同条件下的概率加权求和得到。假设样本空间 S 被划分为两个互斥且穷尽的事件 A 和 A'（如图 3 所示），则事件 B 的概率可以表示为：

3.2 概率的加权求和：全局视角的计算

结合条件概率的乘法法则，全概率公式可以进一步展开为：

这一公式的意义在于，它允许我们通过分析事件 B 在不同条件下的概率，来计算其总体概率。例如，计算 “明天堵车” 的概率，可以分别计算 “明天下雨时堵车的概率” 和 “明天不下雨时堵车的概率”，再根据天气预报中下雨的概率进行加权求和。

四、贝叶斯推断：从先验到后验的认知升级

4.1 先验与后验：概率的迭代更新

贝叶斯推断的核心思想是用新证据更新我们对事件概率的认知。这里的 P (A) 称为先验概率，是我们在获得新证据 B 之前对事件 A 的概率判断；P (A|B) 称为后验概率，是我们在获得新证据 B 之后对事件 A 的概率重新评估。而 P (B|A)/P (B) 则是一个调整因子，它反映了新证据对先验概率的修正程度。

4.2 可能性函数：证据的力量

可能性函数 P (B|A)/P (B) 是贝叶斯推断的关键。它可以大于 1、小于 1 或等于 1，分别表示新证据 B 对事件 A 的支持、削弱或无关。例如，在疾病诊断中，如果某种症状在患者中出现的概率远高于在健康人群中出现的概率，那么该症状的出现就会显著提高患病的后验概率。

4.3 认知的进化：从猜测到科学

贝叶斯推断的过程就像科学家进行实验验证假设一样：先提出一个先验假设，然后通过实验结果（新证据）来修正这个假设。这种迭代更新的思维方式，使得贝叶斯方法在处理不确定性问题时具有独特的优势，能够随着数据的积累不断逼近真实情况。

五、朴素贝叶斯推断：简化的艺术

5.1 条件独立性假设：牺牲精度换取效率

朴素贝叶斯分类器的 “朴素” 之处在于它假设给定类别后，各个特征之间相互独立。这一假设虽然在现实中往往不成立，但却大大简化了计算。例如，在文本分类中，假设每个单词的出现独立于其他单词，我们就可以将文档的概率分解为各个单词概率的乘积：

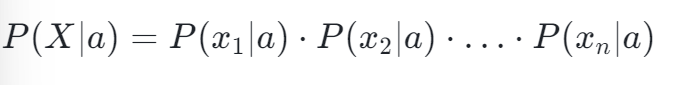
5.2 后验概率的计算：从联合到边缘

结合贝叶斯定理和条件独立性假设，朴素贝叶斯分类器的后验概率可以表示为：

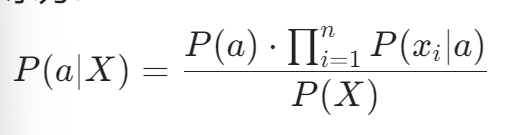
由于 P (X) 对于所有类别来说是相同的，可以忽略不计，因此分类决策仅基于分子部分的比较。这大大降低了计算复杂度，使得朴素贝叶斯在处理高维数据（如文本）时表现出色。

5.3 西瓜分类实战：从理论到实践

让我们通过一个具体的例子来理解朴素贝叶斯的应用。假设我们有一个西瓜数据集，包含纹理、色泽、鼓声三个特征和一个类别标签（好瓜 / 坏瓜）。现在需要判断一个新样本（纹理模糊、色泽乌黑、鼓声浊响）属于好瓜还是坏瓜。

步骤 1：计算先验概率

• 好瓜的先验概率：P (好瓜) = 6/10 = 0.6
• 坏瓜的先验概率：P (坏瓜) = 4/10 = 0.4

步骤 2：计算条件概率

• 纹理模糊 | 好瓜：3/6 = 0.5（好瓜中纹理模糊的数量为 3）
• 色泽乌黑 | 好瓜：2/6 ≈ 0.333（好瓜中色泽乌黑的数量为 2）
• 鼓声浊响 | 好瓜：3/6 = 0.5（好瓜中鼓声浊响的数量为 3）
• 纹理模糊 | 坏瓜：3/4 = 0.75（坏瓜中纹理模糊的数量为 3）
• 色泽乌黑 | 坏瓜：3/4 = 0.75（坏瓜中色泽乌黑的数量为 3）
• 鼓声浊响 | 坏瓜：2/4 = 0.5（坏瓜中鼓声浊响的数量为 2）

步骤 3：计算分子部分

• 好瓜的分子：0.6 × 0.5 × 0.333 × 0.5 ≈ 0.05
• 坏瓜的分子：0.4 × 0.75 × 0.75 × 0.5 ≈ 0.1125

步骤 4：比较分子大小

由于 0.1125 > 0.05，因此判断该样本为坏瓜。

六、拉普拉斯平滑：避免零概率陷阱

6.1 零概率问题：数据稀疏的挑战

在实际应用中，我们经常会遇到某些特征值在训练集中从未与某个类别同时出现的情况。例如，在西瓜数据集中，如果 “色泽淡白” 从未出现在好瓜中，那么 P (色泽淡白 | 好瓜) 就会被计算为 0，导致整个后验概率为 0，无论其他特征如何。

6.2 平滑技术：赋予零概率新生命

拉普拉斯平滑通过在每个特征的计数上加上一个平滑参数 α（通常取 1），来避免零概率的出现。假设我们有 m 个特征，则条件概率的计算公式变为：

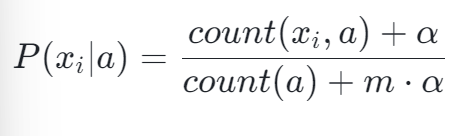
例如，在计算 “色泽淡白 | 好瓜” 的概率时，如果 count (色泽淡白，好瓜)=0，count (好瓜)=6，m=3（纹理、色泽、鼓声），则：

 P

6.3 参数选择的艺术：α 的权衡

α 的取值直接影响平滑的强度。当 α=0 时，不进行平滑，可能导致零概率问题；当 α 增大时，平滑效果增强，但会降低训练数据的权重。在实际应用中，通常通过交叉验证来选择最优的 α 值，以平衡模型的偏差和方差。

七、sklearn 实现：从理论到代码的跨越

7.1 算法选择：不同数据类型的适配

sklearn 提供了多种朴素贝叶斯分类器，适用于不同类型的数据：

• MultinomialNB：适用于离散特征，如文本分类中的词频计数。
• GaussianNB：适用于连续特征，假设特征服从高斯分布。
• BernoulliNB：适用于二值特征，如文本分类中的单词存在与否。

7.2 鸢尾花分类实战：代码全解析

以下是使用 MultinomialNB 对鸢尾花数据集进行分类的完整代码：

7.3 模型评估：超越准确率的维度

除了准确率，我们还可以使用其他指标来评估模型性能，如精确率、召回率、F1 值等。例如，在类别不平衡的情况下，F1 值能更全面地反映模型的性能。此外，概率校准曲线和布里尔分数可以帮助我们评估模型预测概率的可靠性。

八、从朴素到进阶：贝叶斯方法的进化

8.1 半朴素贝叶斯：放松独立性假设

为了缓解朴素贝叶斯的强假设问题，研究人员提出了半朴素贝叶斯方法。例如，TAN（Tree Augmented Naive Bayes）算法通过构建最大带权生成树来捕捉特征之间的依赖关系，既保留了朴素贝叶斯的高效性，又提高了分类精度。

8.2 集成学习：集体智慧的力量

将多个朴素贝叶斯分类器进行集成，可以进一步提升性能。例如，AODE（Averaged One-Dependence Estimators）通过平均多个独依赖分类器的预测结果，减少了单一模型的偏差。

8.3 与深度学习的结合：前沿探索

近年来，研究人员开始探索将贝叶斯方法与深度学习相结合。例如，贝叶斯神经网络通过引入概率分布来表示模型参数的不确定性，在不确定性量化和小样本学习中表现出独特优势。

九、应用场景：朴素贝叶斯的舞台

9.1 文本分类：信息筛选的利器

朴素贝叶斯在文本分类中表现出色，尤其是在垃圾邮件过滤、新闻分类等任务中。其高效性和可解释性使其成为工业界的首选方案之一。

9.2 医疗诊断：辅助决策的助手

在医疗领域，朴素贝叶斯可以通过分析患者的症状、病史等特征，辅助医生进行疾病诊断。其概率输出为医生提供了量化的参考依据。

9.3 金融风控：风险评估的基石

在金融风控中，朴素贝叶斯可以用于评估客户的信用风险。通过分析客户的交易记录、信用历史等特征，模型能够预测违约概率，为金融机构提供决策支持。

十、总结：贝叶斯哲学的启示

朴素贝叶斯算法不仅是一种机器学习技术，更是一种思维方式。它教会我们如何在不确定性中做出最优决策，如何用新证据更新我们的认知，如何在简化假设和复杂现实之间找到平衡。

从概率理论的基石到实际应用的代码，从简单的西瓜分类到复杂的文本处理，我们一路探索了朴素贝叶斯的原理、实现和优化。希望通过本文的学习，你不仅掌握了这门技术，更能体会到数据科学的魅力 —— 用数学的严谨和工程的智慧，从数据中提炼出有价值的洞察。

未来，随着数据量的爆炸式增长和计算能力的不断提升，贝叶斯方法必将在更多领域发挥重要作用。让我们保持好奇心，继续探索数据科学的未知领域，用概率的语言书写更精彩的未来！