【论文精读】基于共识的分布式量子分解算法用于考虑最优传输线切换的安全约束机组组合

本次分析的论文《Consensus‐Based Distributed Quantum Decomposition Algorithm for Security‐Constrained Unit Commitment Considering Optimal Transmission Switching》于2025年6月25日在《Advanced Quantum Technologies》期刊上公开发表。本文提出了一个新的基于共识的分布式量子分解算法，旨在解决电力系统中的机组组合与最优输电开关的联合优化问题。该研究着重于提高电力系统的安全性和经济性，并通过量子计算方法大幅提高了求解效率，能够为电力行业提供更为高效的优化工具。

一、研究背景

在电力系统中，机组组合（Unit Commitment, UC）和最优传输线切换（Optimal Transmission Switching, OTS）是两个关键的优化问题。UC问题主要确定日前机组调度计划，在满足安全约束的前提下最小化电力系统的总运行成本；OTS则致力于通过优化传输线路的开关状态，调整电网拓扑结构，以缓解潮流拥堵、提高系统可靠性。

传统上这两个问题往往被独立处理，但随着电力系统规模的扩大和复杂性的增加，二者之间的相互影响日益显著。一方面，UC和OTS的数学模型中均包含大量的二元变量和连续变量，属于混合整数非线性规划（MINLP）问题，具有离散性、非线性和非凸性，属于典型NP-hard问题，计算复杂度随系统规模呈指数级增长；另一方面，传统的集中式优化方法在处理大规模系统时计算效率低下，难以满足实际运行的需求。

量子计算作为一种新兴的计算范式，为解决UC和OTS的联合优化难题提供了新的思路和方法。基于此，本论文提出了一种考虑UC与OTS联合优化的动态模型，为提高安全约束下该联合优化模型的求解效率，提出了一种基于共识的分布式量子分解算法（Consensus-Based Distributed Quantum Decomposition Algorithm, QDA）。具体工作包括：

（1）针对UC和OTS的联合优化问题，引入了集中式QDA算法，该算法将问题分解为一个优化机组调度的上层UC模块、一个解决潮流约束和拓扑优化的下层OTS模块，以及一个考虑意外场景的故障验证模块，模块间的迭代交互通过添加割平面实现，最终实现动态电网拓扑切换以避免违反安全约束，同时降低运行成本；

（2）在上层UC模块中，利用UC子问题（SP）的对偶信息，基于广义Benders框架构建最优性和可行性割平面。在下层OTS模块中，受灵敏度分析启发，将传输线切换状态对系统运行成本或潮流越限的影响定义为灵敏度，并基于此分析构建了线性最优性和可行性割平面，以及将这些割平面转化为适用于量子计算的QUBO模型（割平面哈密顿量）方法；

（3）在集中式算法的基础上提出了求解效率更高的基于共识的分布式QDA。该算法使用相邻节点的相角和交互功率作为共识变量，允许每个节点独立并行地求解带共识约束的局部问题；同时构建局部割平面哈密顿量，将主问题（MP）解耦到节点级别的局部主问题（local MPs），局部MPs的规模小于集中式MP，其并行求解特性显著提高了联合优化问题的求解效率。

二、UC与OTS联合优化模型

2.1 问题描述

因为UC问题负责机组调度计划，OTS旨在确定最优电力系统拓扑，当电网拓扑改变时，先前计划的机组调度可能不再适用，导致电网拓扑与机组调度计划之间存在潜在的相互依赖关系，同时该模型必须考虑日前故障约束以确保系统的稳定性和可靠性。

论文首先建立了UC和OTS的联合优化模型，该模型的目标函数为最小化系统总运行成本，包括机组燃料成本、启动成本和输电线路开关成本，此联合优化模型涉及连续变量（如机组出力和线路潮流）和离散变量（如机组启停状态和传输线切换状态），是一个MINLP问题，表述形式如下：

$$\underset{P,U}{\min }\sum _{t=1}^{NT}\left[\sum _{i=1}^{NG}\mathcal{K}(P_{i,t})+\mathcal{J}(U_{i,t})+\sum _{l=1}^{NL}\mathcal{L}(Z_{l,t})\right]$$

其中，$\mathcal{K}(P_{i,t})$为机组燃料成本，$\mathcal{J}(U_{i,t})$为机组启动成本，$\mathcal{L}(Z_{l,t})$为传输线转换成本。

约束条件包括：

（1）功率平衡约束

即各节点的功率注入等于负荷需求：

$$\sum _{i\in NG(n)}{P}_{i,t}-\sum _{l\in N{L}_{\text{from}}(n)}{\vec{P}}_{l,t}+\sum _{l\in N{L}_{\text{to}}(n)}{\vec{P}}_{l,t}=D_{n,t},\forall n,\forall t$$

（2）机组输出功率约束

机组输出功率在最小和最大限制之间，且受启停状态影响：

$$P_i^{\min }\cdot U_{i,t}\cdot {\tilde{U}}_{i,t}^c\le P_{i,t}\le P_i^{\max }\cdot U_{i,t}\cdot {\tilde{U}}_{i,t}^c,\forall i,\forall t$$

（3）机组最小启停时间约束

确保机组在指定持续时间内保持开/关状态：

$$\sum _{j=t-T_i^{\text{on}}}^{t-1}{U}_{i,j}\ge T_i^{\text{on}}{U}_{i,t-1}(1-U_{i,t}),\forall i,\forall t\ge T_i^{\text{on}}$$

$$\sum _{j=t-T_i^{\text{off}}}^{t-1}(1-U_{i,j})\ge T_i^{\text{off}}{U}_{i,t}(1-U_{i,t-1}),\forall i,\forall t\ge T_i^{\text{off}}$$

（4）输电线路潮流容量约束

即考虑线路容量限制遵循基尔霍夫定律：

$$-P_l^{\max }\cdot Z_{l,t}\cdot {\tilde{Z}}_{l,t}^c\le {\vec{P}}_{l,t}\le P_l^{\max }\cdot Z_{l,t}\cdot {\tilde{Z}}_{l,t}^c,\forall l,\forall t$$

$$({\vec{\theta }}_{n,t}-{\vec{\theta }}_{m,t})/x_l-{\vec{P}}_{l,t}\le M(2-Z_{l,t}-{\tilde{Z}}_l^c),\forall l(n\to m),\forall t$$

$$({\vec{\theta }}_{n,t}-{\vec{\theta }}_{m,t})/x_l-{\vec{P}}_{l,t}\ge -M(2-Z_{l,t}-{\tilde{Z}}_{l,t}^c),\forall l(n\to m),\forall t$$

（5）防孤岛约束

即确保当所有相关线路均可切换时，至少有一条输电线路连接到每个节点：

$$\sum _{l\in NL(n)}{Z}_{l,t}\ge 1,\forall n,\forall t$$

2.2 基于共识的分布式量子分解算法

本论文提出的基于共识的分布式量子分解算法（QDA）是集中式量子分解算法的分布式版本，采用多阶段优化策略，将联合优化问题分解为上层UC模块、下层OTS模块和故障验证模块，并通过构建割平面实现模块间的迭代交互，最终获得接近全局最优的解。分布式方法与集中式方法的整体框架是相同的，主要区别在于局部优化子问题（SPs）的模型构建和求解过程，如图1所示。

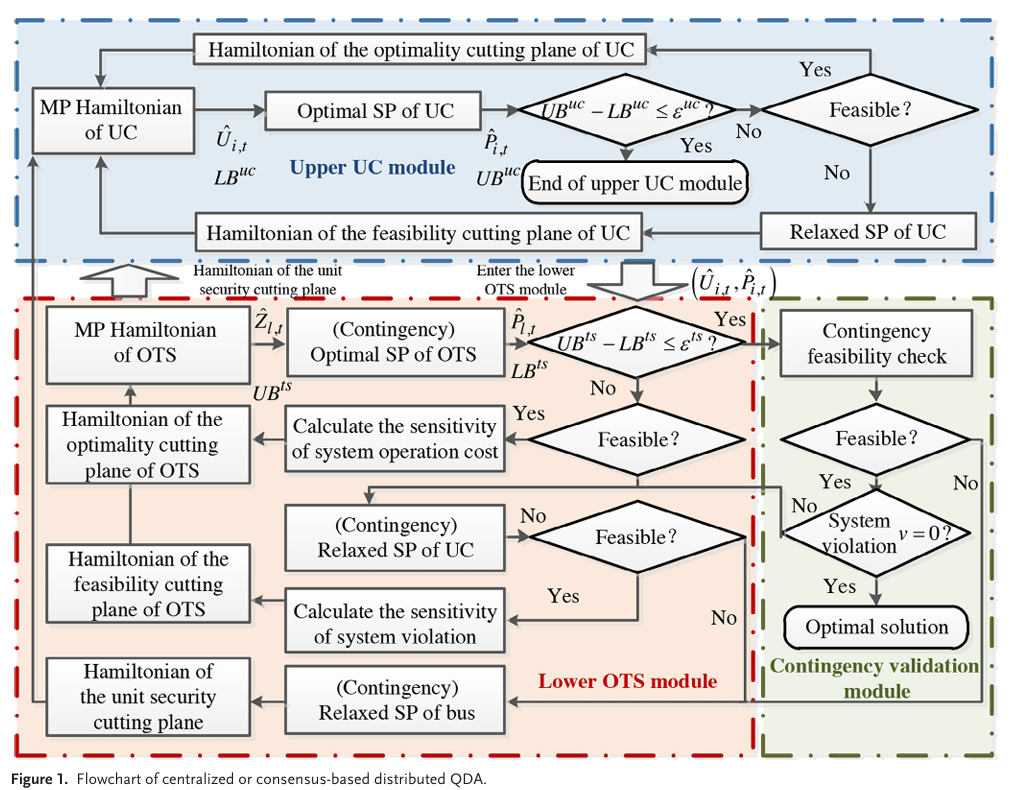
上层UC模块生成机组调度计划后传递给下层OTS模块以确定符合安全检查并适配机组调度计划的最优电网拓扑；如果下层OTS模块始终无法满足安全验证标准，则构建机组的安全割平面并返回上层模块以调整机组调度，此迭代过程逐步使机组调度和电网拓扑趋向于接近全局最优解；故障验证模块充当反应式智能纠错机制，防止N-1故障引起的安全问题。前缀“contingency”表示约束考虑故障情况的变体形式。

UC和OTS模块的主问题（MPs）负责优化二元决策变量，即机组启停状态和输电线路状态。这些是离散优化问题，求解计算复杂度随离散变量数量呈指数增长，由于量子计算在加速求解约束组合优化问题方面的潜力，本论文将UC和OTS模块的主问题（MPs）重新表述为QUBO格式的哈密顿量，从而利用量子退火器和相干光量子计算机来高效求解。基于共识的分布式QDA将共识变量（节点间功率交换和相角）引入UC的最优子问题（SPs）、OTS的最优子问题（SPs）和OTS的松弛子问题（SPs），允许这些子问题（SPs）在节点级别解耦；共识约束的添加确保共识变量通过迭代共识过程逐步收敛，从局部子问题导出的对偶变量、连续变量、系统成本和约束违反情况可用于构建局部割平面，进一步确保主问题（MPs）的可解耦性。因此，解耦后的局部主问题（local MPs）中的二元变量数量显著减少，促进了更高效的求解过程。

2.2.1 上层UC模块

上层UC模块负责确定日前最优机组调度计划，主要包括以下几个部分：

（1）基于共识的局部最优子问题（SP）

局部UC最优子问题（SP）负责求解连续变量$P_{i,t}$，同时验证机组启停状态${\hat{U}}_{i,t}$的可行性。将UC问题分解为各节点的本地最优SP，以相邻节点间的功率交换作为共识变量，通过软约束将本地共识变量与全局共识变量的偏差纳入目标函数，最小化目标函数以确保局部共识变量逐渐收敛到全局共识变量。

$$\min \sum _{i=1}^{NG(n)}\sum _{t=1}^{NT}\mathcal{K}(P_{i,t})+\sum _{m\in {\mathcal{N}}_{\text{ad}}(n)}\mathcal{M}({\vec{P}}_{n,m}^n,{\vec{P}}_{n,m}^{+})$$

其中，$\mathcal{M}$为共识偏差，包含对偶变量和惩罚系数。

（2）UC的松弛子问题（SP）

当最优SP不可行时，论文引入了连续松弛变量$(S_{i,t}^2,S_{i,t}^1)$来量化机组在$t$时段违反功率输出约束的程度，从而构建松弛SP。类似于局部UC最优子问题（SP），原始松弛UC子问题（SP）利用平均共识方法分解来构建局部松弛UC子问题（SP），由每个节点独立求解，局部松弛UC子问题（SP）表达式为：

$$min{\mu }^{\prime }=\sum _{i=1}^{NG}\sum _{t=1}^{NT}(S_{i,t}^1+S_{i,t}^2)+\sum _{m\in N_{ad}(n)}\mathcal{M}({\vec{P}}_{n,m}^n,{\vec{P}}_{n,m}^{+})$$

为避免多个局部松弛子问题（SPs）之间复杂的共识迭代，并实现松弛变量的更快最优分配，论文构建了一个反映成本信息的松弛变量目标函数。同时原始松弛子问题（SP）的Karush-Kuhn-Tucker（KKT）条件也被作为约束之一包含在内，同时也考虑了松弛变量的约束，从而导出了改进的共识启发式UC松弛子问题（SP）：

$$\min \mu =\sum _{i=1}^{NG}\sum _{t=1}^{NT}\mathcal{K}(S_{i,t}^1)+\mathcal{K}(S_{i,t}^2)$$

该目标函数结合了发电成本系数，以在当前机组启停状态下实现最小违反成本$\mu$，确保松弛变量优先分配给发电成本较低的机组。由于原始松弛子问题（SP）满足凸优化条件，通过将KKT条件作为约束纳入共识启发式松弛子问题（SP）可以确保系统违反量的最优性。此外，它结合了面向经济的违反成本目标函数和约束中的松弛变量边界，指导松弛变量在不同节点间的分配，以符合机组的发电成本特性。因此，整个共识启发式松弛子问题（SP）的目的是在最小化系统违反量的同时，优先将违反量分配给运行成本较低机组的功率约束。

（3）局部UC主问题（MP）

基于共识的UC最优子问题（SP）和改进的UC松弛子问题（SP）都在节点级别返回局部割平面，因此可以构建节点级的局部UC主问题（MP）。因为主问题考虑了每个节点内与二元变量相关的约束，为解决此约束组合优化问题，本论文将主问题（MP）重新表述为Ising模型并采用量子退火器和CIM来加速求解。

完成所有节点的局部主问题（MP）和子问题（SPs）之间的内部迭代后，将获得一个机组调度计划$({\hat{U}}_{i,t},{\hat{P}}_{i,t})$。该调度计划随后传输到下层OTS模块，如果机组调度不满足输电线路的潮流安全约束，下层OTS模块中的下层内部迭代将生成相应的最优电网拓扑。

2.2.2 下层OTS模块

在集中式和分布式框架中，下层OTS模块首先通过OTS的最优子问题（SP）评估所有安全约束是否满足。如果安全约束满足，则构建最优性割平面并返回给OTS的主问题（MP）；如果安全约束不满足，则求解OTS的松弛子问题（SP），然后构建可行性割平面，进而返回给OTS的主问题（MP）。

OTS的主问题（MP）受二元变量约束以及最优性和可行性割平面的约束，它侧重于优化这些二元变量并为原联合优化问题的目标函数提供一个下界。如果子问题（SPs）没有可行解，则表明对于给定的机组调度无法找到合适的电网拓扑。在这种情况下，下层模块将求解节点的松弛子问题（SP），并构建一个机组安全割平面返回给上层模块以修正机组调度。

与基于共识的上层UC模块不同，下层模块的子问题（SPs）将考虑在实际电网拓扑下与相邻节点相关的共识变量。

（1）局部OTS最优子问题（SP）

基于上层模块确定的机组启停状态${\hat{U}}_{i,t}$ ，需要对当前的传输线切换计划${\hat{Z}}_{l,t}$进行安全检查。OTS的最优子问题（SP）将二元变量${\hat{U}}_{i,t}$和${\hat{Z}}_{l,t}$作为固定输入，负责优化联合优化问题中的连续决策变量$p_{i,t}$和$p_{l,t}$：

$$\underset{P}{\min }{w}_n=\sum _{t=1}^{NT}\left[\sum _{i\in NG(n)}\mathcal{J}({\hat{U}}_{i,t})+\mathcal{K}(P_{i,t})+\sum _{l\in NL(n)}\mathcal{L}(Z_{l,t})\right]+\sum _{l\in NL(n)}\mathcal{I}({\vec{P}}_l^n,{\vec{P}}_l^{+})+\sum _{m\in {\mathcal{N}}_{\text{ad}}(n)}\mathcal{O}({\vec{\theta }}_m^n,{\theta }_m^{+})$$

节点级的局部OTS最优子问题 (SP)不仅需要考虑该节点与其相邻节点之间输电线路的功率流，还需要考虑该功率流与相邻节点相角之间的关系。因此，OTS最优SP引入了两种类型的共识变量：

• ${\vec{P}}_l^{+}$和${\theta }_m^{+}$是全局共识变量，分别代表连接到节点$n$的输电线路$l$的功率流和相邻节点$m$的相角；

• ${\vec{P}}_l^n$和${\vec{\theta }}_m^n$是局部共识变量，它们分别是节点$n$的局部最优SP中相邻节点功率流和相角的副本。

功率流共识约束和相角共识约束以共识偏差$\mathcal{I}$和$\mathcal{O}$的形式表示为软约束，并被纳入目标函数的表达中。OTS的最优SP考虑了节点拓扑的功率平衡约束、机组输出功率容量约束、输电线路功率流容量约束、以及潮流方程，一旦每个节点的局部共识变量收敛，OTS的局部最优SP就趋近于全局最优解。

受Benders框架中割平面构建和灵敏度分析方法的启发，本论文基于系统运行成本对输电线路状态的灵敏度，开发了一种类似于Benders割平面公式的OTS最优性割平面。首先确定在给定机组调度和当前电网拓扑下节点的运行成本，然后在当前拓扑下逐一临时修改输电线路的状态，并重新计算拓扑变化后节点的运行成本，由此由于输电线路的状态变化而产生的系统运行成本变化被定义为系统运行成本的灵敏度。如果输电线路状态的临时更改导致解不可行或形成电气孤岛，则系统运行成本对该输电线路的灵敏度设为0。

如果子问题（SP）没有可行解，则表明在确定的机组调度下，当前电网拓扑未能通过安全检查。在这种情况下，需要引入松弛变量来构建OTS的松弛子问题（SP）。

（2）局部OTS松弛子问题（SP）

基于局部OTS最优子问题（SP），将机组功率容量约束和输电线路潮流容量约束松弛，以构建局部OTS松弛子问题（SP），可能产生可行解。类似于局部OTS最优子问题（SP），此松弛子问题（SP）使用二元变量${\hat{U}}_{i,t}$和${\hat{Z}}_{l,t}$作为固定输入，并引入两类共识变量${\vec{P}}_l^n$和${\vec{\theta }}_m^n$，以及它们对应的软共识约束。在指定的机组和输电线路状态下，此子问题（SP）负责最小化局部系统违反量，其数学公式表示如下：

$$\min v_n=\sum _{t=1}^{NT}\left[\sum _{i\in NG(n)}S{}_{i,t}^{-}+S{}_{i,t}^{+}+\sum _{l\in NL(n)}{F}_{l,t}^{-}+F_{l,t}^{+}\right]+\sum _{l\in NL(n)}\mathcal{I}({\vec{P}}_l^n,{\vec{P}}_l^{+})+\sum _{m\in {\mathcal{N}}_{\text{ad}}(n)}\mathcal{O}({\vec{\theta }}_m^n,{\theta }_m^{+})$$

其中，机组容量松弛变量$S{}_{i,t}^{-}$和$S{}_{i,t}^{+}$分别代表节点$i$在时段$t$机组的下松弛功率和上松弛功率；输电线路容量松弛变量$F_{l,t}^{-}$和$F_{l,t}^{+}$分别代表节点$l$在时段$t$输电线路 的下松弛潮流和上松弛潮流；所有松弛变量的总和代表节点 $n$的局部系统违反量$v_n$。

如果OTS的松弛SP有解，则表明可以通过传输线路切换为该机组调度方案构建一个合适的电网拓扑。类似于局部最优OTS的SP中使用的方法，可以计算节点$n$的系统违反量对每条输电线路状态的灵敏度，此灵敏度随后可用于构建OTS 的局部可行性切割平面；如果OTS的松弛子问题（SP）仍然无解，则表明无法为上层UC模块提供的机组调度方案找到可行的电网拓扑。在这种情况下，有必要返回到上层UC模块的UC主问题(MP)以调整机组调度方案。

（3）节点松弛子问题（SP）

节点松弛SP通过松弛节点功率平衡约束来确保可行性，其做法是将所有输电线路固定为连通状态，同时将上层UC模块提供的机组启停状态${\hat{U}}_{i,t}$作为等式约束赋给变量$U_{i,t}$，并计算相应的拉格朗日乘子${\hat{\lambda }}_{i,t}$，该松弛SP计算在完全连通状态和上层机组调度方案下的最小功率平衡过载量，表达如下：

$$min\varpi =\sum _{t=1}^{NT}\sum _{n=1}^{NB}{R}_{n,t}^{-}+R_{n,t}^{+}$$

求解该表达式可得到功率平衡约束的最小违反量以及与机组调度约束对应的拉格朗日乘子，如此能够构建机组安全切割平面，该切割平面通过外部环返回并添加到上层模块的UC 主问题（MP）中，以此优化机组调度方案：

$$0\ge \hat{\varpi }+\sum _{i=1}^{NG}\sum _{t=1}^{NT}{\hat{\lambda }}_{i,t}(U_{i,t}-{\hat{U}}_{i,t})$$

（4）局部OTS主问题（MP）

局部OTS主问题负责确定连接到节点$n$的输电线路的二进制状态变量$Z_{l,t},l\in NL(n)$。它提供了与上层机组调度相匹配的最优部分电网拓扑，并给出联合优化问题目标函数的局部下界。该主问题表述如下：

$$min{h}_n+\sum _{l=1}^{NL(n)}\sum _{t=1}^{NT}\mathcal{L}\left(Z_{l,t}\right)$$

由于在松弛的OTS子问题（SP）中，目标函数和约束在时间周期之间是独立的，因此从该子问题生成割平面的可行性自然可以在这些时间周期上解耦。

2.2.3 故障验证模块

故障验证模块将代表N-1故障的参数${\tilde{U}}_{i,t}^c,{\tilde{Z}}_{l,t}^c$纳入相关约束，如上文中图1的流程图所示，流程从故障可行性检查开始：

• 如果在此检查中未识别到可行解，则表明仅通过输电线路切换无法在给定故障下防止违反安全约束。在这种情况下，有必要为节点的故障松弛子问题（SP）构建一个机组安全割平面，并返回给上层UC模块以调整对应于该故障的机组调度；

• 如果确实存在可行解，则下一步是评估故障场景下的系统违反量是否为零。如果检测到零违反，则表明当前的机组调度和电网拓扑在故障下仍然有效，然后输出最优解。如果存在违反，则流程进入下层OTS模块的故障松弛OTS子问题（SP），通过该模块的内部迭代重新校准电网拓扑。

故障可行性检查将正常条件下的最优UC解$({\hat{U}}_{i,t},{\hat{P}}_{i,t})$和相应的电网拓扑$({\hat{Z}}_{l,t},{\hat{P}}_{l,t})$作为固定输入，同时考虑意外故障施加的约束，此过程的数学公式如下：

$$\min v_c=\sum _{t=1}^{NT}\left[\sum _{i\in NG}S{}_{i,t}^{-}+S{}_{i,t}^{+}+\sum _{l\in NL}{F}_{l,t}^{-}+F_{l,t}^{+}\right]$$

按照图1流程所示，故障可行性检查有三种可能情况：

• 如果存在可行解且代表故障下系统违反量的目标函数等于零，则表明故障可行性检查已通过，在正常条件下得出的最优机组调度和电网拓扑仍然适用于该故障场景；

• 如果存在可行解但系统违反量非零，则流程移至下层OTS模块中基于共识的局部松弛OTS子问题（SP），其中约束（机组功率容量约束、输电线路潮流容量约束、潮流约束）被调整为反映故障条件，然后重新执行下层OTS模块的内部迭代过程，以在故障下重新校准电网拓扑；

• 如果未找到可行解，则构建一个机组安全割平面，然后传回上层UC模块以在故障下调整机组调度，涉及内部和外环（与正常条件下的程序相同，但相关约束需根据故障场景进行修改）的上下模块之间的此迭代过程持续进行，直到获得满足故障可行性检查的最优解。

总之，故障验证模块旨在将正常条件下得出的最优解智能校正为故障后场景的最优响应。

2.3 基于量子计算的主问题（MP）哈密顿量优化方法

为了利用量子计算的并行特性来加速特定问题的求解，论文重新表述了UC或OTS主问题（MP）中的割平面为QUBO形式的哈密顿量，同时还提出了一种将机组最小开/停机约束转化为QUBO形式哈密顿量作为惩罚项的新方法，该方法代数化地处理机组最小开/停机约束，避免引入辅助变量，从而显著减小主问题（MP）的QUBO矩阵规模。

2.3.1 割平面QUBO哈密顿量构建

本论文将MP中的各类割平面（UC最优性割平面、UC可行性割平面、OTS最优性割平面、OTS可行性割平面和机组安全割平面）转换为QUBO形式的哈密顿量。

以UC最优性割平面的QUBO哈密顿量为例，其表达如下：

$$H_n^{\text{UC, op}}=\sum _{i=1}^{NG(n)}\sum _{t=1}^{NT}\left[\sum _{e=1}^{N{E}^{\text{UC}}}{F}_{e,i,t}^{\text{UC, op}}+{\xi }_n^{\text{UC, op}}(C_e^{\text{UC, op}}-U{B}_e^{\text{UC}})F_{e,i,t}^{\text{UC, op}}\right]\cdot U_{i,t}+\sum _{i=1}^{NG(n)}\sum _{t=1}^{NT}\sum _{i^{\prime }=1}^{NG(n)}\sum _{t^{\prime }=1}^{NT}\left(\sum _{e=1}^{N{E}^{\text{UC}}}{F}_{e,i,t}^{\text{UC, op}}{F}_{e,i^{\prime },t^{\prime }}^{\text{UC, op}}\right)U_{i,t}{U}_{i^{\prime },t^{\prime }}$$

其中，$H_n^{\text{UC, op}}$表示节点$n$的UC最优性割平面的哈密顿量；$N{E}^{\text{UC}}$表示上层UC模块的内部迭代次数；$C_e^{\text{UC, op}}$是第$e$次迭代期间UC最优性割平面的常数项；$F_{e,i,t}^{\text{UC, op}}$指第$e$次迭代最优性割平面中二元变量$U_{i,t}$的系数；$U{B}_e^{\text{UC}}$表示第$e$次迭代上层UC模块目标函数的上界；${\xi }_n^{\text{UC, op}}$是在将CU最优性割平面转换为QUBO形式时引入的惩罚项系数。

2.3.2 改进的机组最小启停时间约束QUBO哈密顿量

机组最小开/停机约束是耦合多个时间段的复杂二元变量约束，负责防止机组运行状态的突变。当考虑这些约束时，机组的启动和停机决策不仅受当前时段需求的影响，还受前后时段状态的影响，这种时间依赖性引入了强烈的时段间耦合，显著增加了决策的复杂性。从根本上讲，最小开/停机约束是离散的、非线性的不等式约束，使模型优化复杂化，尤其是在具有许多变量的大规模模型中，对计算时间和资源的需求急剧增加。

本论文在所有时间段$T$上的UC和OTS联合优化问题中，引入了$2\ast T$个机组最小开/停机约束。在传统的惩罚构造方法中，需要一组辅助二元变量来将这些约束等价地转化为非线性等式约束，然后将这些等式约束平方作为惩罚项，但这会引入了大量的辅助变量，因此迫切需要一种不依赖辅助变量的机组最小启停时间约束的惩罚构造方法。

由前文机组最小启停时间约束可得，每项涉及的二进制变量数量分别为$T_i^{on}+2$和$T_i^{off}+2$，为了减少这个数量，可将复杂的机组最小启停时间约束分解为每个时间段的更简单约束：

Ui,t(1−Ui,t−1)≤Ui,τ,τ∈[t+1,min⁡{t+Tion,NT}]U_{i,t} (1 - U_{i,t-1}) \leq U_{i,\tau}, \tau \in \left[ t + 1, \min \left\{ t + T_i^{on}, NT \right\} \right] Ui,t​(1−Ui,t−1​)≤Ui,τ​,τ∈[t+1,min{t+Tion​,NT}]

$$U_{i,t-1}(1-U_{i,t})\le 1-U_{i,\tau },\tau \in \left[t+1,\min \left\{t+T_i^{off},NT\right\}\right]$$

基于机组最小启停时间约束，上述公式将每个原始约束分别分解为$T_i^{on}$和$T_i^{off}$个约束，增加了最小启停时间约束的数量，同时将每个约束中的二进制变量数量减少到三个，从而降低了每个约束的复杂性。

在简化了机组最小启停时间约束之后，论文将该两个约束耦合到一个统一的公式中，使用$(-U_{i,t}+U_{i,t-1}$来表示机组的状态转换。具体来说，如果机组$i$在时段$t$停机，则$(-U_{i,t}+U_{i,t-1})=1$；如果机组$i$在时段$t$启动，则$(-U_{i,t}+U_{i,t-1})=0$；如果机组状态保持不变，则$(-U_{i,t}+U_{i,t-1})=0$。鉴于$U_{i,\tau }$的期望值为0或1，可以为时段$t$构造一个惩罚项，使得当机组在当前时段停机时，令$U_{i,\tau }=0$；当机组在当前时段启动时，令$U_{i,\tau }=1$；当机组状态未改变时，不施加特定惩罚。这种方法开发了一种满足机组最小启停时间约束且无需辅助变量的QUBO哈密顿量：

$$H^{\text{QT}}={\xi }^{\text{QT}}{\left[U_{i,\tau }+(-U_{i,t}+U_{i,t-1})-0.5\right]}^2$$

简化后为：

$$H^{\text{QT}}=2{\xi }^{\text{QT}}\left(U_{i,t}-U_{i,t-1}{U}_{i,t}+U_{i,t-1}{U}_{i,\tau }-U_{i,t}{U}_{i,\tau }\right)$$

这种方法避免了引入辅助变量，大幅减小了QUBO矩阵的规模，降低了量子资源需求。

2.3.3 MP哈密顿量的优化求解

通过对割平面哈密顿量和机组最小启停时间约束哈密顿量相加，即可得到与UC和OTS的MP等价的QUBO形式哈密顿量：

$$H^{UC}=H^{UC,op}+H^{UC,fea}+H^{SE}+H^{QT}$$

$$H^{TS}=\sum _{l=1}^{NL(n)}\sum _{t=1}^{NT}\mathcal{L}\left(Z_{l,t}\right)+H^{TS,op}+H^{TS,fea}$$

这种 QUBO 形式的MP哈密顿量可以很容易地转化为适用于量子计算的伊辛模型（Ising model），从而使用量子退火器和基于光学系统的相干伊辛机（CIM）的硬件上，实现快速高效的问题求解。求解该模型的目标是找到伊辛哈密顿量的基态，该基态对应于运行成本最小的电力系统最优状态。

三、实验验证与结果分析

本论文提出了一种基于多分解和共识策略的、可扩展的分布式求解方法（Distributed QDA）来解决UC和OTS的联合优化问题，由于涉及跨区域潮流作为共识变量，优化问题可以在区域级别解耦并独立求解，适用于大规模、跨区域的电力系统。而根据电力系统场景，在QDA框架内进行多分解后，每个模块内的优化子问题不一定采用共识策略，而是可以使用全局建模方法（Centralized QDA）求解，更适用于较小规模、集中统一调度的场景。

本论文使用6节点系统（6-Bus System）和IEEE RTS 24节点系统（IEEE RTS 24-Bus System）进行了多种场景分析。鉴于6节点系统的结构相对简单，在6节点系统上使用集中式 QDA（Centralized QDA）来验证算法流程的正确性和可行性，在确认了集中式方法的有效性后，使用IEEE RTS 24节点系统展示基于共识的分布式 QDA（Distributed QDA）的优越性。

实验中，所有SP使用Gurobi9求解，MP转换为QUBO问题后在D-Wave量子退火平台和玻色量子相干光量子计算机上实现。

3.1 6节点系统实验结果

• 场景1：仅考虑UC，不考虑传输约束和潮流方程；

场景1中通过比较平均共识机制和共识启发式松弛SP的求解时间，验证了分布式QDA中的共识启发式方法的效率优势，其求解时间仅为平均共识机制总时间的1.78%；

• 场景2：考虑传输约束和潮流方程的UC以及全连接的固定传输网络拓扑，同时考虑了两个子场景：分默认线路容量和降低线路容量两种子场景；

场景2中随着线路容量的降低，系统运行成本增加，验证了传输约束对机组调度的影响。

• 场景3：UC和OTS联合优化模型，同时考虑两个子场景：使用默认线路潮流限制和降低线路潮流限制；

联合优化相比固定拓扑的UC，运行成本显著降低，证明了OTS在缓解潮流拥堵、降低成本方面的有效性。

• 场景4：考虑N-1故障条件下的UC和OTS联合优化模型，目标通过机组调度和线路切换的紧急调整来适应意外线路故障，从而确保节点负载得到满足而不会出现大幅削减。

在N-1故障情况下，联合优化能够通过调整线路开关状态和机组调度，有效应对故障，保证系统安全运行，尽管成本有所增加，但仍优于传统方法。

3.2 IEEE RTS 24节点系统实验结果

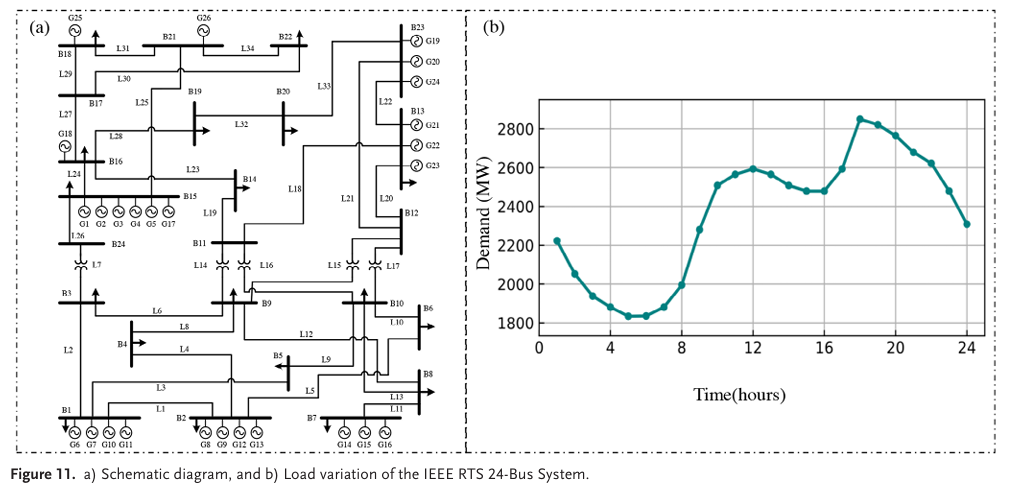
图11a展示了IEEE RTS 24节点系统的示意图，图11b展示了IEEE RTS 24节点系统在不同时间段的负载变化。

• 场景5：UC和OTS联合优化，最终的线路状态是全连接；

在场景5中，如图所示结果，分布式QDA与商业求解器Gurobi9获得了相同的最优解，但求解时间更短，验证了算法的有效性。

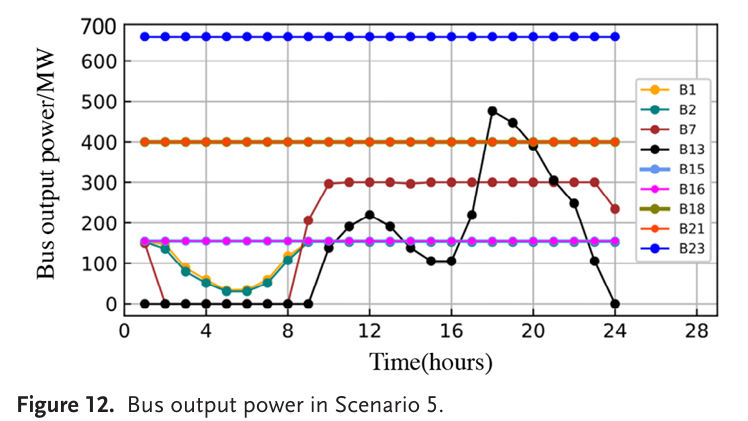
• 场景6：降低线路潮流限制的UC和OTS联合优化；

在场景5的基础上，场景6将线路（L1-L34）的潮流限制从其原始值降低了80MW。虽然这种降低在全连接线路配置下导致无可行解，但UC和OTS的联合优化模型找到了可行解。如图所示，在降低线路潮流限制的情况下，分布式QDA获得了比Gurobi9更优的解，计算值降低了0.003%，且求解时间显著缩短，证明了算法在处理复杂约束时的优势。

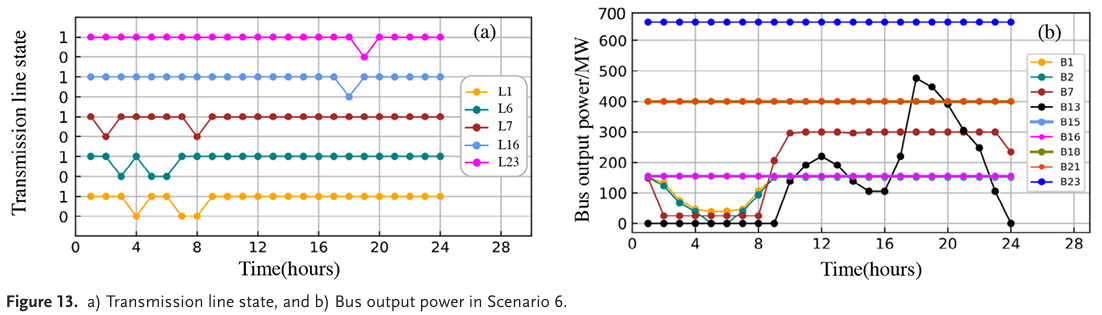
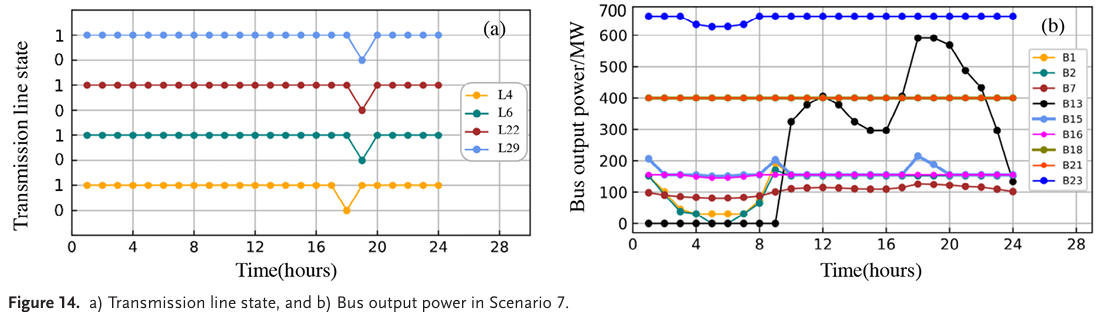
• 场景7：考虑N-1故障的UC和OTS联合优化；

该场景在场景6的设置基础上，假设线路L10因故障离线，进而具有固定传输拓扑的传统UC模型仍然不可行，但UC和OTS的联合优化模型找到了可行解。结果如图所示，分布式QDA能够快速找到可行解，运行成本相比Gurobi9降低0.34%，展示了算法的优越性。

3.3 综合比较

对于6节点系统，由于规模相对较小且结构简单，无需应用分布式QDA，集中式QDA足以验证工作流的有效性。对于更大更复杂的IEEE RTS 24节点系统，集中式方法难以在合理时间内收敛到可行解，因此采用基于共识的分布式QDA来展示其计算效率。

最优输电开关问题OTS仅从场景3及以后才涉及，因此CIM 用于场景3之后开始求解MP哈密顿量。在迭代过程中，MP 中割平面的数量随迭代次数线性增加，理论上导致优化复杂度逐渐增加，求解速度变慢。本论文仅在最后一次迭代中求解QUBO形式的 MP，并将其求解时间视为每次迭代求解MP所需时间的上界。这种方式能够估计量子处理单元（QPU）使用时间和总计算时间的上限，既具有成本效益，又足以验证算法的有效性，同时也突出了CIM的量子优势。

通过对6节点系统和IEEE RTS 24节点系统模型在场景1到7的详细计算结果综合比较中，可以得到以下结论：

在6节点系统结果中，使用集中式QDA获得的目标函数值与Gurobi9相同（场景4的结果更优）。然而，D-Wave和CIM版本的QDA相比Gurobi9需要更多的计算时间来收敛。

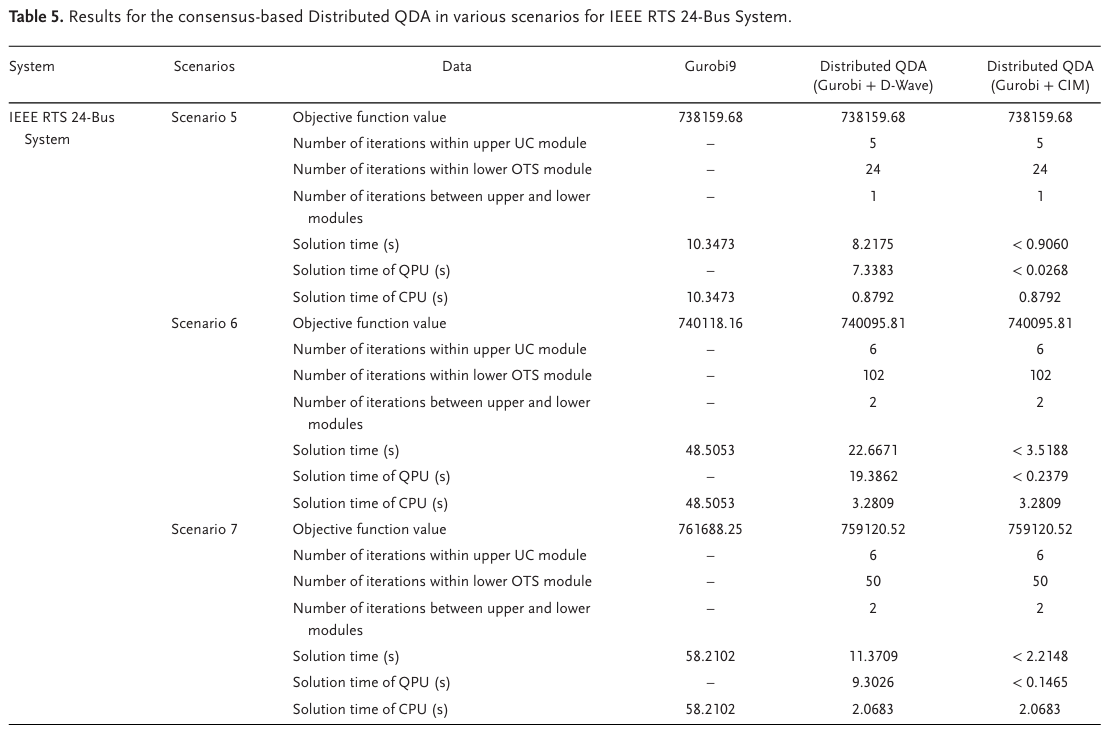
在IEEE RTS 24节点系统的结果表明，基于共识的分布式QDA始终获得与Gurobi9相等或更优的目标函数值（在场景6和7中结果更优）。此外，所有场景的收敛时间都显著短于Gurobi9，其中CIM实现的分布式QDA在求解速度上优于D-Wave版本。这些结论进一步强调了相干光量子计算机在优化领域的潜力，也证明了分布式 QDA 的有效性和优越性。

四、讨论与总结

为了解决考虑日前事故约束的UC和OTS联合优化问题，本论文提出了集中式和基于共识的分布式量子分解算法（QDAs），利用量子计算的优势来求解QUBO问题。

本文的贡献主要体现在以下方面：

（1）提出了一种基于共识的分布式量子分解算法（QDA），用于解决考虑最优输电开关的安全约束机组组合问题，实现了电网拓扑和机组输出功率的协调优化，为提高发电的经济性和安全性提供了灵活可靠的解决方案；

（2）设计了多阶段优化策略，通过上层UC模块、下层OTS模块和故障验证模块的迭代交互，逐步逼近全局最优解，还将计算时间减少到平均共识机制所需时间的1.78%；构成主问题（MP）的割平面被依次转化为QUBO形式的哈密顿量，使得MP的离散变量优化能够利用相干光量子计算机（CIM）进行加速计算，显著提高了算法的优化速度；

（3）改进了机组最小启停时间约束的QUBO哈密顿量构建方法，无需辅助变量，大大减小了问题规模，提高了量子计算的效率；

（4）实验结果表明，分布式QDA在求解效率和解的质量上均优于传统的Gurobi9，特别是在大规模系统和复杂约束条件下，优势更加明显。

总体而言，本文通过实现机组组合与最优输电开关的联合优化，有效降低系统运行成本，提高电力系统的安全性和可靠性，为电力企业带来显著经济效益同时保障电力供应的稳定性，为电力系统的经济运行和规划可提供更为精确和高效的优化工具。

论文链接：Consensus‐Based Distributed Quantum Decomposition Algorithm for Security‐Constrained Unit Commitment Considering Optimal Transmission Switching - Huang - Advanced Quantum Technologies - Wiley Online Library