【SAS求解多元回归方程】REG多元回归分析-多元二次回归
多元二次回归是线性回归的扩展形式,通过引入自变量的二次项和交互项来捕捉非线性关系。适用于因变量与多个自变量之间存在曲线或交互效应的情况。其模型形式比简单线性回归更复杂,能够拟合更灵活的数据模式。
目录
【示例】
数据预处理
基本语法
SAS代码
逐步选择
编辑
参数估计
方差分析
回归统计量
y的拟合诊断
y的回归变量值-残差值
【示例】
设Y与有相关关系,考虑二次回归模型
,8组观测数据如下:

数据预处理
根据二次模型要求处理数据集得到新数据集

基本语法
PROC REG data = 数据集;
MODEL 因变量 = 自变量列表 </可选项>;
< restrict 自变量的等式约束;>
SAS代码
针对处理后的数据
data d1;input x1-x9 y ;cards;
38 47.5 23 1444 2256.25 529 1805.00 1805.00 1092.50 66.0
41 21.3 17 1681 453.69 289 873.30 873.30 362.10 43.0
34 36.5 21 1156 1332.25 441 1241.00 1241.00 766.50 36.0
35 18.0 14 1225 324.00 196 630.00 630.00 252.00 23.0
31 29.5 11 961 870.25 121 914.50 914.50 324.50 27.0
34 14.2 9 1156 201.64 81 482.80 482.80 127.80 14.0
29 21.0 4 841 441.00 16 609.00 609.00 84.00 12.0
32 10.0 8 1024 100.00 64 320.00 320.00 80.00 7.6
;
proc print;
run;
proc reg data=d1;model y=x1-x9 /selection=stepwisesle=0.05 sls=0.05;
run;
proc reg data=d1;model y=x4 x7;
run;
quit;
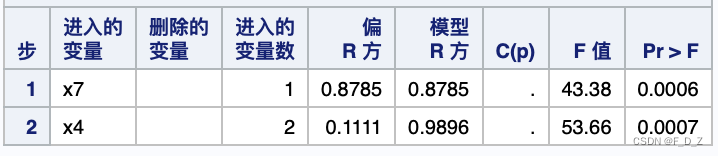
逐步选择
第一步

第二步

直到留在模型中的所有变量的显著性水平都为 0.0500,同时没有其他变量满足 0.0500 显著性水平。
得到x4、x7,对应于
参数估计

所以二次回归方程为:
参数估计表不仅给出回归方程的系数,还给出检验的结果(显著性概率p值)
比如给定, 若常数项和自变量的p值均
a,意味着与回归方程高度显著产生矛盾,为了得到最优回归方程,应从方程中删除最不重要的自变量,重新建立
与其余自变量的回归方程后再检验,这就是变量筛选的意义所在。
方差分析

回归平方和:
残差平方和:
均方误差:
均方误差是模型中误差方差的估计
检验统计量,显著性概率p值小于
,这表示拟合的模型是高度显著的,该模型解释了这组数据总变差中的主要部分。
回归统计量

决定系数:
复相关系数:
标准差的估计量:
y的拟合诊断

y的回归变量值-残差值