[科研理论]机器人路径规划算法总结及fast_planner经典算法解读
本文介绍一篇路径规划的综述来总结划分目前大部分路径规划算法,并介绍fast_planner论文理论知识。
文章目录
- 1 路径规划综述
- 1.1 Reactive Computing/被动式算法
- 1.1.1 被动式动作
- 1.1.2 局部优化方法
- 1.2 Soft-Computing/智能算法
- 1.2.1 进化计算
- 1.2.2 人工智能
- 1.3 C-Space-Search/构型空间搜索算法
- 1.3.1 图搜索
- 1.3.2 基于采样方法
- 1.4 Optimal-Control-Based/基于优化控制的算法
- 1.4.1 偏微分方程求解(PDE Solving)
- 1.4.2 数值优化(Numerical Optimization)
- 2. fast_planner详细笔记
- 2.1 动力学路径搜索(前端)
- 2.1.1 Hybrid A*完整解释
- 2.1.2 特殊函数
- 2.1.2.1 扩展函数
- 2.1.2.2 成本计算和启发值计算
- 2.2 轨迹优化(后端)
- 2.2.1 均匀B样条
- 2.2.2 优化问题构建
- 2.2.3 优化问题求解
- 2.3 时间重分配
1 路径规划综述
路径规划算法很多,我这里选择了一篇把各种算法都归类的综述(若有推荐其他更好更全面的,烦请告知_),文中也指出了一个问题,就是在学习这些算法的时候不用纠结于某某算法到底是全局规划还是局部规划(前端还是后端),有些算法是可以灵活调整的,只是某些算法的特殊性经常被用在某某位置,比如DWA(动态窗口算法)既可以用于局部也可以用于全局规划。

根据文献Path Planning for Autonomous Mobile Robots: A Review,一文的划分,他将path planning划分为四大类Reactive Computing (被动式算法), Soft Computing (智能算法), C-Space Search (构型空间搜索) 和 Optimal Control (基于优化控制算法),我翻译不当可以看原文,中文名字可能有点意义不明确。
1.1 Reactive Computing/被动式算法
被动式算法通常用作局部路径规划器,负责覆盖机器人周边环境并进行动态重规划。这类算法的优势在于能快速处理新信息(例如新探测到的障碍物),这些信息通常来源于有限的机载传感器。作为局部规划器,它们通常规划机器人的下一个直接动作或机动策略,以避开附近障碍物,同时尽量遵循由全局规划算法生成的路径指引。然而,这类算法也可能陷入局部最小值。根据实现方式,反应式计算算法可进一步分为两类:反应式机动方法,其根据障碍物的存在直接决定机器人的下一个机动动作;以及局部优化方法,其依据障碍物信息对现有路径进行优化调整。
1.1.1 被动式动作
这种方法根据原理分为两种:基于场的方法以及基于评估输入的方法。
基于场的方法包括 Artificial Potential Fields(人工势场法APF)以及 Artificial Potential Fields(向量直方图VFH)。在APF算法中,机器人运动是由来自外部环境(比如障碍物)的虚拟力的合力所驱动的。简单来说,障碍物对机器人产生“斥力”,把它推开,从而避免碰撞;而目标位置则会对机器人产生“引力”,把它吸引过去。这种力的分布可以参考图中的示意图。

Ge 和 Cui 曾经将APF应用到动态障碍物环境下的避障中。不过这个方法有一个常见的问题:容易让机器人卡在所谓的“局部最小点”上,也就是一个机器人既远离不了障碍,也接近不了目标的尴尬位置。为了克服这个问题,后续有不少研究做了改进。Vadakkepat 等人就是为了这个目的,他们把APF和遗传算法(进化算法)结合起来,解决卡死的问题。这种组合方式还被用在了一个六轮模拟探测车的路径规划中。此外,还有人尝试把粒子群算法(PSO)和APF结合,形成了另一种混合方法。
** VFH(向量场直方图)算法**,这是由 Borenstein 提出的。它的核心思想是建立一个极坐标直方图,来判断机器人周围障碍物的分布密度,然后选一个障碍最少的方向前进,如下图所示。后来这个方法也被很多人改进过,让它更加智能和稳定。


Bug算法包括Bug1和Bug2,它们的思路非常简单:当机器人遇到障碍物时,就绕着它走,直到能继续朝目标前进为止。这两个版本的主要区别在于:Bug1要求机器人沿着整个障碍物边界绕一圈(见图6a),而Bug2只需要部分绕行,一旦有机会朝目标前进就直接离开障碍继续走了。Bug系列算法的优点是实现简单、计算量极低,几乎不考虑路径最优性。适用于那种只带有简单传感器、只能感知周围障碍物的机器人。在执行时,机器人要么直奔目标,要么沿着碰到的障碍物边界走。

接下来是一些会直接输出速度指令的避障方法:其中最有代表性的就是速度障碍法(Velocity Obstacles, VO),它会同时考虑机器人和动态障碍物的速度向量,从而判断哪些速度会导致碰撞。比如图5b中展示的那样,构造一个“碰撞锥”,只要机器人当前速度不在这个锥体范围内,就能安全避障。
另外一个非常经典的方法是动态窗口法(Dynamic Window Approach, DWA)。它的核心思想是:在一定的时间窗口内,在速度空间中搜索一个速度组合,使机器人可以沿着无碰撞的圆弧路径前进。虽然这种方法不是全局最优,但局部规划效果很好,而且即使是高速移动的机器人也能用。Feng 等人对DWA做了改进,通过缩小搜索空间来减少计算量。还有一些研究把它用于节能路径规划。虽然DWA通常被用作局部路径规划器,但 Zhang 等人提出了一种在全局路径规划中使用DWA的方式。
1.1.2 局部优化方法
这类算法通常是在已有路径的基础上,根据环境中的障碍物对路径进行调整。
它们的设计重点是尽量减少计算量,即使会因此牺牲路径的最优性,甚至可能无法保证最终一定能到达目标点(也就是牺牲“完备性”)。常见的调整方法包括:在速度空间中选择不同的速度曲线,或者让路径在“虚拟力”的作用下拉伸、延展等。其中一个经典方法是Elastic Bands(弹性带)路径优化算法,由 Quinlan 和 Khatib 提出 。它的基本思想是:把原来的无碰撞路径看作一条“弹性绳”,然后根据障碍物的位置让这条绳子自动调整,比如被拉直、拉伸,像图6b里那样。这个方法会把路径上的点划分成一系列气泡(Bubble)区域,每个气泡表示一段局部的安全空间。气泡的大小取决于离障碍物的距离——离障碍越近,气泡越小、数量越多。这种方式不仅适用于静态环境,在动态环境下也可以使用,不过如果环境变化太大,这种方法可能会失效。后来这个方法也被扩展到了非完整约束(non-holonomic)的机器人。Khatib 等人通过引入曲率约束,以及使用Bezier曲线来让路径更符合这类车辆的运动特性。在此基础上,还有一个扩展版本叫做Timed Elastic Bands(TEB)。它不仅考虑了路径形状,还引入了“时间”维度,从而满足机器人在实际运动中受到的动力学约束(kinodynamic constraints)。这使得TEB更适合用在需要考虑速度加速度限制的移动机器人上,比如送货机器人或者自动驾驶小车。
1.2 Soft-Computing/智能算法
这一类算法的目标并不是求出精确的最优解,而是尽量逼近它,允许一定程度的误差存在。通常,它们需要用户根据实际环境的特点来手动调参数,调得好效果才会理想。这些方法比较灵活,可以处理动态环境,也适合用于变量多、自由度高的问题。不过,它们的计算开销通常也很大,对硬件性能有一定要求。在这部分内容中,我们参考了 Mirjalili 和 Dong 提出的分类方法,将这类算法分为三类:进化算法(Evolutionary)、模糊控制(Fuzzy Control)和机器学习方法(Machine Learning)。这些控制器非常适合用在环境未知或变化大的情况,可以根据机器人实时感知到的障碍信息动态生成路径。总的来说,智能算法的核心是利用一些可反复调整的模块,比如“个体”(进化算法)、“规则”(模糊控制)或“神经元”(机器学习),来不断优化路径规划结果,让机器人能在复杂或不确定的环境中自主行动。
1.2.1 进化计算
进化算法(Evolutionary Algorithms)也常被称为“元启发式(Meta-heuristic)”或者“自然启发算法(Nature-inspired)”。它们的核心思路,是通过一个“种群”的进化过程来生成路径。这个种群由一群“聪明的个体”组成,它们的行为灵感来自自然界中的各种现象 。这些个体有时会改变自己,也有可能跟其他个体互动。某些情况下,它们甚至会在环境的“自由空间”中进行移动——这个自由空间就是机器人可以到达的区域。经过一系列这样的“进化操作”后,算法会逐渐逼近最优解。路径的生成质量和收敛时间,跟个体的行为策略、环境的复杂程度以及用户设定的参数(比如个体数量)都有关系。常见的进化算法包括遗传算法(Genetic Algorithm)和群体智能优化方法(Swarm Optimizers)。前者模拟“染色体”的概念,后者则模拟自然生物的行为模式。
就像上面提到的,遗传算法的个体被设计成类似染色体的结构。这些染色体由基因组成,通常是二进制数字。这些数字编码了一条路径,也就是一组连续的路径点。所以说,在路径规划问题中,每条染色体其实就是一条路径的代表。图 7a 举了一个用网格来展示的例子:每个网格单元有编号,算法最初会随机生成一些染色体。接下来,这些染色体会经历三个基本过程:繁殖(Reproduction)、交叉(Crossover)和变异(Mutation)。
繁殖就是保留表现最好的个体,淘汰最差的;交叉则是在两个染色体之间交换“基因”;而变异是在某些基因上引入一些随机变化,以鼓励算法去探索搜索空间,避免陷入局部最优解。不断重复这三个步骤,整个群体的解就会逐步优化。

与遗传算法不同,群体智能优化方法(Swarm Optimizers)模拟的是智能体在自由空间中移动和作用的过程。这些“智能体”大多数时候都模仿动物行为。经过多次迭代之后,这些个体朝着目标前进的运动轨迹会逐渐形成一条路径,并最终收敛成一个解。其中,**粒子群优化算法(PSO)**因其原理简单而格外突出,它的灵感来源于鱼群这类动物的群体行为。在这个算法中,一组“粒子”会随着时间推移不断更新自身的位置,最终让算法逐渐收敛。这些粒子在搜索最优位置时会彼此交流信息,并结合自己的过往经验来做出判断。
另一个广为人知的群体智能算法就是蚁群算法(ACO),顾名思义,它模拟的是蚂蚁寻找食物的过程。在觅食时,蚂蚁会在路径上留下信息素,其他蚂蚁则会沿着信息素的轨迹前进。而信息素浓度高的路径,通常代表着一条更优的路线。图 7b 就展示了这种机制:起点和目标之间存在障碍,最终留下信息素最多的路径也就是最短路径。借助这个策略,虚拟的“蚂蚁”可以在网格上自由移动,根据信息素强度决定路径。为了避免陷入局部最优解,一些研究还引入了启发函数来进行辅助。
Che 等人则通过引入“灰狼优化(Grey Wolf Optimizer)”中的一条规则,来进一步改进蚁群算法的收敛能力。Luo 等人则提出了一些改进方案,目的在于避免 ACO 死锁的情况,并加快收敛速度。这种算法也被应用在数字高程模型(DEMs)中,用来最小化路径规划所需的时间和能耗。在动态障碍环境中同样也能适用,Sangeetha 等人的研究就将蚁群算法与模糊控制结合起来,实现了更灵活的路径调整。
当然,还有很多类似的自然启发算法没法一一列举,还有一些研究探索了算法之间的“混合策略”。比如 Saraswathi 等人就提出了一种结合布谷鸟算法和蝙蝠算法的混合模型,并对其效果进行了测试。
1.2.2 人工智能
Soft Computing算法也可以使用其他类型的可调算子,例如模糊规则或神经网络。在这方面,Seraji 和 Howard展示了在一款实验型移动平台上利用模糊逻辑在非结构化地形中实现导航的能力。Zavlangas 和 Tzafestas 则提出了一种基于模糊逻辑的系统,能够使移动机器人自主地在动态环境中穿行,同时避开障碍物。
Wang 等人的研究重点在于解决机器人陷入局部最优位置的问题,比如遇到 U 形障碍物导致的困境。Pandey 等人也开展了使用模糊逻辑进行障碍物规避的仿真实验,并展示了测试结果。在神经网络的应用方面,Yan 和 Li 同样使用了模糊逻辑,不过他们更关注于降低计算资源消耗,并能够适应动态障碍环境。Pandey 和 Parhi 则将模糊逻辑与一种名为“风驱优化”(Wind Driven Optimization)的群体算法相结合,后者被用来调优模糊规则。
关于神经网络的使用,Zou 等人早在 2000 年初就对这类算法在路径规划中的应用做过简要综述。Engedy 和 Horváth提出了一种基于神经网络的路径规划方法,用于让移动机器人避开静态和动态障碍物。Zhang 等人将神经网络用于迷宫类环境中的最短路径寻找。这类技术还被用于与遗传算法相结合的应用中。
文献中还有不少研究将模糊逻辑与神经网络结合使用,方法也各不相同。比如 Mohanty 和 Parhi就采用多种系统联合运行来实现自主导航。关于这些混合算法的更多研究细节与更全面的综述,可参考 Mac 等人的工作。
此外,**强化学习(Reinforcement Learning, RL)**也逐渐成为控制机器人运动的一种研究方向。Faust 等人甚至将 RL 与概率路网法(PRM)相结合,后者是一种将在后文中介绍的路径规划算法。
1.3 C-Space-Search/构型空间搜索算法
本类算法将路径规划器的工作空间视为机器人可达的所有状态或构型所组成的空间。因此,大多数相关研究将该工作空间称为构型空间(Configuration Space,简称 C-Space)。这类算法的核心思想是在该 C-Space 中选取一组离散的样本进行处理。换句话说,就是对 C-Space 进行离散化。这组样本至少包含起始状态和目标状态,或是与它们相对接近的样本。通过这种方式,算法便可以在样本集合中执行搜索操作。最终,算法会找到并返回一组连接起始状态和目标状态的样本子集,这组样本构成了最终生成的路径。换而言之,路径上的每一个路径点都对应于 C-Space 中的一个样本。
这种方法意味着所生成路径的质量在很大程度上取决于这些样本的分布方式、样本间的连接关系以及搜索策略。事实上,正因为这种依赖性,在某些方法中还需对生成的路径进行后处理,以使路径更加平滑。
根据对 C-Space 进行离散化的方式不同,C-Space 搜索算法可进一步划分为两类:图搜索(Graph Search)算法与采样法(Sampling-Based)算法。图搜索方法使用一个预定义的图结构(如图2所示)来完成 C-Space 的离散化。该图中的每一个节点代表一个 C-Space 中的样本,并通过边与其相邻节点相连。而采样法则通过迭代方式在 C-Space 中动态创建和/或调整样本。这类算法在找到一条可行路径之后,仍可以继续优化,以期寻找更优解。

1.3.1 图搜索
如前所述,C-Space 可以以图的形式进行离散化。图搜索(Graph Search)算法通过完全或部分地遍历该图,寻找一条连接起始状态和目标状态的路径。最早的一类图搜索算法所生成的路径,其路径点均位于相邻样本之上。换言之,路径中相邻路径点之间的连接恰好对应图中的边。图 8a 示意了这种情形,路径的形状完全由图结构中的边所决定。因此,本文将生成此类路径的图搜索算法归类为“边约束型”(Edge-restricted)算法。这类路径的质量与图的结构密切相关。
图结构通常采用单元分解(Cell Decomposition)或路线图(Roadmap)等形式。然而,图结构的边约束会限制路径的灵活性。为解决该问题,研究人员提出了“任意角度”(Any-angle)图搜索算法。之所以命名为“任意角度”,是因为边约束型路径只能采用某些特定的朝向值。例如,在一个八邻域的规则网格中(如图 8a 所示),边约束路径的朝向角只能为 0、±45、±90、±135 和 180 度。而任意角度算法则打破了这一限制,其生成的路径点不必位于相邻节点上,因此路径可以呈现出更加灵活和自然的走向。图 8b 展示了一个任意角度路径的示意图。

关于边约束型(Edge-restricted)算法,图 9 展示了文献中最具代表性的几种版本。其中最为知名且基础的边约束路径规划算法是 Dijkstra 算法。该算法以起点或终点之一作为初始节点,并向其邻居传播信息。这些信息可以是从起点到当前节点的代价,也可以是到达终点所需的剩余代价。算法通过迭代方式访问已访问节点的邻居节点,不断传播代价信息,并为每个访问节点分配其父节点。如果环境允许(即不存在将起点或终点隔离的障碍物),算法最终会访问到两个端点。此时,可通过回溯父节点的方式提取路径,即从最后一个被访问的节点开始,沿着父节点逐步回溯至起点。

前方知识高密度区域:多年后,Hart 等人提出了启发式版本 A 算法,以加快计算速度。随后,D 算法(Dynamic A)被提出 ,作为 A 的一种增量式扩展。增量性意味着当代价图发生变化时,算法能够重用先前的计算结果,避免从头开始重新计算,从而在机器人遇到新障碍时实现快速重规划。D* 的改进版本 Focused D* 在计算时间上进一步优化。Koenig 和 Likhachev提出了另一种 A* 的增量式扩展——Lifelong Planning A*(LPA*),在此基础上又发展出一种更为简洁的 D* 版本,即 D*-Lite。Colas 等人将该算法应用于移动机器人搜索与救援任务中。
由于 A* 及其各种 D* 变体依赖启发式函数,因此生成的路径可能并非最优。Likhachev 等人 提出了一种“任意时间”版本,即允许算法在限定时间内输出当前最优路径。Dolgov 等人则提出了 Hybrid A*,作为 A* 的一种可行性优先版本,其通过在路径找到后对节点进行重构,使得最终路径满足运动学约束,尽管这会牺牲部分最优性和完备性。
关于任意角度(Any-angle)算法,Field-D* 算法是其中最早提出的算法之一,因其被应用于 NASA 的火星探测车(例如 Spirit 和 Opportunity)而广为人知。与 D* 和 D*-Lite 类似,Field-D* 也是一种增量式算法,可在后续执行中重复利用先前计算结果。尽管 Field-D* 在解决边约束问题方面表现出色,仍有进一步优化路径的空间。随后,研究者提出了更多以 A* 为基础的任意角度算法,专注于在避障的前提下寻找最短路径。Nash 等人 提出了 Theta* 算法,包括两种版本:计算开销较小的 Base-Theta* 与精度更高、路径更接近全局最优的 Angle-Propagation Theta*。Theta* 的核心思想是在障碍物转角处尽可能减少朝向变化,这与 Field-D* 相比具有更优的路径平滑性。
Base-Theta* 的增量版本被称为 Incremental Phi*,而 Lazy-Theta* 则是其运行速度更快的变体,由 Nash 等人提出。此外,Theta* 也被拓展用于非均匀代价地图,其中靠近障碍物的位置具有更高代价。Šišlák 等人提出了 Accelerated A* 算法,尽管计算速度稍慢,但所生成路径比 Theta* 更短。Yap 等人提出了 Block A* 算法,并将其性能与 A* 和 Theta* 进行了对比。Nash 和 Koenig进一步比较了 Accelerated A*、Block A*、Field-D* 和 Theta* 等算法及其变体,并在后续工作中将这些算法与可见图(visibility graphs)进行比较。
Muñoz 和 R-Moreno提出了 S-Theta* 算法,以实现更平滑的朝向变化。3DANA 算法则用于在高程地图上生成路径。此外,还有其他一些相较于 Theta* 和其他任意角度算法表现更优的算法,包括 Any-angle Subgoal Graphs与 Anya。
1.3.2 基于采样方法
采样法路径规划算法通过遵循不同的策略,在配置空间(C-Space)中依次生成样本。在满足某一条件或一组条件(例如达到时间限制)后,从生成的样本中提取路径。该类算法具有渐近最优性,即随着时间的推移,通过生成更多样本逐步逼近最优解。一般而言,这类算法适用于高维空间的搜索。然而,为了接近全局最优解,通常需要生成大量样本,从而对内存资源提出较高需求。
若仅考虑两个关键点(起始位置或状态与目标位置),则该算法被归类为单次查询(single-query)算法;若针对同一环境考虑多个点,则归为多次查询(multiple-query)算法。就单次查询而言,最著名的算法之一是快速随机树(Rapidly-exploring Random Tree, RRT)算法,它也是快速确定性树(Rapidly Deterministic Tree, RDT)的一种特殊形式。该算法模拟树状结构的生长过程,从起始点出发动态生成样本,仿佛树枝般不断扩展。
图10a展示了该过程的示意图。当某个样本与目标之间的距离小于预设阈值时,可通过回溯路径直至起点来提取可行路径。如前所述,算法仍可继续执行迭代,以寻找更优路径。针对RRT算法的多个改进版本已在文献中提出。Kuffner与LaValle提出了双向版本,命名为RRT-Connect。此后,Yershova等人提出动态域RRT(Dynamic Domain RRT)算法,在树的扩展过程中引入障碍物感知机制。Arslan与Tsiotras 借鉴图搜索算法LPA的思想,提出了RRT#,在收敛速度上优于传统RRT算法。Karaman与Frazzoli提出启发式RRT(RRT*),在保持渐近最优性的同时提高了计算效率。
RRT的性能随后得到了进一步改进。Informed RRT算法在找到一条可行路径后,以一椭圆形区域(包围起点与目标)限制搜索范围,从而避免无效探索,提高搜索效率。Gammell等人提出批量信息树(Batch Informed Trees, BIT*)算法,并通过实验验证其性能优于RRT*、Informed RRT以及FMT。BIT同样借鉴了图搜索算法LPA的一些思想。区域加速批量信息树(AIT*)进一步提升了BIT在狭窄通道场景下的性能。后续提出的自适应信息树(Adaptively Informed Trees, AIT)和高级批量信息树(Advanced Batch Informed Trees, ABIT*)进一步优化了BIT*算法,并被集成于NASA的一项实验性探测车中。

多查询(multiple-query)采样算法,最经典的要数概率路线图法(PRM)了 。这个算法一开始会在配置空间(C-Space)中分布一些初始采样点,然后再从这些点出发生成更多采样,相当于从每个点都“长”出一棵小树。图 10b 形象地展示了这个过程的基本原理。接下来,通常会用像 A 这样的图搜索算法,在这张“路线图”里找到一条从起点到终点的路径。后来,Karaman 和 Frazzoli 还对 PRM 做了改进,引入了启发式的方法,提高了算法的计算效率。Park 等人 提出了一个更高效的版本,使用分层结构(hierarchical structure)来减少所需采样点的数量,但依然保持良好的连通性。Alenezi 等人也验证了 PRM 在室内机器人模拟场景中的效果。除此之外,Ichter 等人还把 PRM 和强化学习结合起来,提出了关键点PRM(Critical PRM)*,这个方法会优先考虑一些“关键区域”,比如狭窄通道之类的地方,从而提高规划效果。
还有一个值得一提的算法是 快速行进树(FMT),它的目标是加快 RRT 和 PRM 的收敛速度,同时还能处理自由度很高的问题。它不仅吸收了 RRT 和 PRM 的一些特点,还参考了一个叫做快速行进法(FMM)的最优控制算法。为了进一步加快计算速度,Ichter 等人又提出了 群体行进树(GMT),这是 FMT* 的一个并行化版本,能利用 GPU 进行加速。最后,还有一些结合了动态采样和模型预测控制(MPC)的方法,这类混合算法可以在路径规划中更好地考虑运动学和动力学约束,也正在逐步成为研究热点。
1.4 Optimal-Control-Based/基于优化控制的算法
基于优化控制的方法(Control Approach based algorithms)的核心思想,是通过设计一个控制函数,让机器人从配置空间(C-Space)中的初始状态顺利移动到目标位置。顾名思义,这类路径规划方法是从最优控制(Optimal Control)的角度来解决问题的。
它和“软计算”类方法的最大不同在于:这里没有什么可调参数,而是要求你把问题完整地定义清楚,包括状态空间、动力学约束、目标函数等等。根据求解方式的不同,这类方法可以分为两个子类:
- 偏微分方程求解类(PDE Solving):这类算法基于动态规划原理(Dynamic Programming Principle, DPP),在一个网格上求解偏微分方程(PDE),进而得到路径。可以理解为在整张地图上“慢慢扩散”,直到找到最优解。
- 数值优化类(Numerical Optimization):这里的思路是先有一条初始路径(可能是任意生成的),然后在考虑机器人动力学约束的前提下,对这条路径进行优化,让它变成一个真正可行、甚至更优的解。
1.4.1 偏微分方程求解(PDE Solving)
在最优控制方法中,有一类是基于动态规划原理(Dynamic Programming Principle, DPP),通过在网格上求解Hamilton–Jacobi–Bellman(HJB)方程来做路径规划的。因为这是个偏微分方程(PDE),所以我们把这种方法叫做PDE求解类路径规划方法。
你可以把它想象成:在网格上模拟一圈波从起点向外扩散,每个网格点被分配一个“波到达的时间值”,而波的扩散速度会根据你设计的代价函数以及HJB方程的形式来决定。但这类算法一个明显的缺点是:它们一般很难处理不连续的约束条件,比如突然出现的障碍或动态变化的边界。
HJB方程中有一个特殊版本,叫做Eikonal方程。它是静态的,只返回一个标量值(即某位置的代价),波的传播速度只和这个位置的值有关。它的一个非常棒的特点是:路径的方向刚好和总代价函数的梯度一致,所以你可以用一个简单的梯度下降法把最优路径找出来。为了解决这个问题并降低计算量,研究者们提出了一整套叫“Fast Methods”的方法,其中最有名的就是 Fast Marching Method(FMM),由 Sethian 提出。FMM 的思路有点像 Dijkstra 算法,会依次“访问”每个网格节点,不过它不是用距离来更新每个点的值,而是用解出的 Eikonal 方程结果。结果就是:你得到的是一条平滑、连续并且全局最优的路径。

Fast Marching Method(FMM)在处理方向相关的代价(也叫各向异性代价)时会出现次优解。所谓方向相关的代价,意思是波的传播速度不仅受位置影响,还跟传播方向有关 —— 也就是说,每个点上分配的是一个向量代价。不过,在某些特定情况下,即使有点各向异性,FMM 还是可以给出比较准的结果,比如代价函数大多数沿着坐标轴方向变化的场景。这类情况就像图 11b 展示的那样。为了解决更通用的静态 HJB 方程问题,Sethian 和 Vladimirsky 提出了 Ordered Upwind Method(OUM)算法。Shum 等人也验证了 OUM 的收敛性。OUM 的主要缺点是:计算代价会随着场景中各向异性的程度增加而上升,也就是说,越复杂的代价方向性,算起来越慢。Shum 等人在另一项研究中还将 HJB 应用于带有各向异性特征的路径规划中,考虑了能量最小化和路径稳定性,还把坡度的方向和大小都纳入考虑。
还有一种方法叫做** Fast Sweeping Method(FSM)**,也被证明可以用于求解通用静态 HJB 方程。FSM 的核心思想是:反复沿特定方向访问整个网格的所有节点,所以计算上迭代次数会很多。Takei 和 Tsai 用 FSM 来处理考虑转弯半径限制的 HJB 方程。如果是 Eikonal 方程,Bak 等人 对 FSM 做了加速优化,用于应对代价函数变化剧烈的情况。Detrixhe 等人还做了一个并行版本,进一步加快计算速度。Jeong 和 Whitaker提出了另一个适合并行架构的算法,叫做 Fast Iterative Method(FIM),也是专门用来求解 Eikonal 方程的。
1.4.2 数值优化(Numerical Optimization)
这一小类方法主要是在已有的可行路径基础上进行优化。跟我们之前在 3.1 节提到的“局部优化”不同,这里讲的是“全局优化”。它的目标是让最后得到的路径在全局范围内最优,不过代价是需要更大的计算量。Ratliff 等人 提出的方法是先用 RRT 或 PRM 这类采样规划方法生成一条初步可行的路径,然后再用梯度优化技术(比如梯度下降)来逼近最优路径。Plonski 等人则考虑了一种更特别的情况:机器人在太阳能地图中移动,同时还要动态调整路径来最大化光照,方便充电。他们用 DP 来实时规划路径。Ajanović 等人 把 DP 和模型预测控制(MPC)结合,规划出更节能的路径,这在电动车或太阳能车里很实用。除了这些方法,还有一些比较有意思的,比如:
- bang-bang 控制方法 ,一种经典的最优控制策略;
- 混合整数线性规划(MILP),适合处理带有开关决策或障碍约束的优化问题。
最后值得一提的是,Kogan 和 Murray 提出了一种非线性优化方法,专门用来规划时间最优路径,路径长度一般在 20 到 70 米之间,适合中短距离的高效路径规划。
2. fast_planner详细笔记
fast_planner是经典的无人机规划算法,周博宇老师这个算法的框架我认为无论从理论层面还是代码工程层面都能够经得起考验,并且该算法拥有较为经典的前后端、建图等模块,适合初学者研究,后续的ego_planner确实很强,但是少了建ESDF图以及前端搜索的基本避障功能,将这些功能都移到后端优化中,我觉得可以把fast_planner看懂之后再学。代码链接,论文链接。
后面公式排版太乱,可移步语雀查看:无人机路径规划问题。
2.1 动力学路径搜索(前端)
这里就用的是前文中构型空间搜索的Hybrid A*算法,能够规划出一条满足动力学约束的前端路径,降低后端优化的压力,其具体流程是这样的:

这里的P和C是A*的开集和闭集的概念,先完整的解释一下这个伪代码(以下描述为伪代码的一条条解释,慢慢读应该很好理解),后面再详细说明某些函数。
2.1.1 Hybrid A*完整解释
首先初始化地图大小,分配变量及大小等等;判断开集中是否为空,如果不为空,进入主循环;从开集的点中取出代价最小的点n_c,并且把n_c加入到闭集中;判断n_c是否到达终点或者n_c有无碰撞直达终点的扩展路径(这个概念应该最早是从Hybrid A*的论文中提出的,可以更快的找到路径,比如全是空地就不用一格一格的搜索,而是直达终点),如果满足条件直接返回此时的路径;从n_c根据动力学约束扩展点,这个扩展过程需要满足无人机的动力学约束;然后因为我们的预测点不是按照栅格来的,所以需要修剪一下同一栅格内的预测点,根据预测点的代价,选择最低的代价作为当前栅格的点,然后把扩展的栅格添加到扩展集nodes中;在nodes中遍历;如果扩展集当前点n_i没有在闭集中(没在当前路径中),而且没有碰到障碍物(这里的代码中其实就是查栅格地图中是否有障碍物);计算扩展集当前点n_i的g_i并加上当前节点n_c的代价,如果扩展集当前点n_i没有在开集中就加到开集中;如果扩展集当前点n_i在开集中,判断通过当前路径的代价是否比之前那条路径的代价大,如果大于,那么不动这个路径,直接进行下次扩展集点n_{i+1}的处理(这一步其实就是扩展点扩到了之前的开集上了,然后判断哪个路径最优,选择最优的情况);如果扩展集当前点n_i没有在开集中,或者在开集中,但是代价更小,那么将当前节点n_i作为扩展集当前点n_i的父系节点,g_{temp}作为代价;并根据 Pontryagin 极小值求得启发值作为最终f_c值。
我觉的A*几乎可以概括为扩展和评估两大步骤。评估分为评估当前开集和评估当前扩展点集。
2.1.2 特殊函数
2.1.2.1 扩展函数
这里没有单独规划无人机的Yaw角,只规划了三维位置,因为本算法认为yaw可以从平面位置差分出来,一般来说是适用的,但是如果有特殊任务(比如巡检)我感觉可以修改成单独规划yaw角。文中将轨迹定义为

这里用的K次多项式表达x、y、z的位置,一般用的是五次多项式,五次多项式有六个待求解系数,首尾各三个边界值(位置、速度、加速度)刚好能够求出,且C^2光滑性质在无人机中已经足够了。在扩展阶段,fast_planner就使用不同的加速度、不同的时间间隔来遍历推导下一步无人机的位置,这个推导阶段就是假设无人机是一个线性时不变系统,根据这个公式推导:

猛地一看不知是啥(其实还是挺面熟的,信号与系统、现控中见过),其实就是位置等于之前的位置加上现在的激励。
2.1.2.2 成本计算和启发值计算
A*算法中最重要的就是实际成本和启发值计算,这个g是实际成本,h是启发值,f是综合成本,对于同一节点他们有这样的关系:

这个实际成本g在这里定义为

对应程序中的离散处理后为

主要意思就是时间最短,输入加速度更小。
然后是求解启发值h,这个启发值是A*算法的一大特点,能够引导算法快速的前往目标点,启发值计算使用了庞特里亚金极小值原理(Pontryagin’s Minimum Principle, PMP)。

由这里可见,在计算启发值时,其实使用的是三次多项式轨迹,降低问题的复杂性,成本用的是跟之前一样的,只不过时把状态方程带入了,顺便一提,A的那个提前结束搜索机制也是根据这个来计算的,只不过要检查是否有碰撞,所以PMP由于有闭式解,计算很快,经常用于这样的场合即问题能够被简单化理论化,路径无复杂约束。当然Hybrid A作者也提出这个提前退出机制如果在每一个点都进行查询,会比较费时,所以引入了概率,即每个点有概率被查询,降低了计算量。
2.2 轨迹优化(后端)
在讨论后端之前,先对比一下轨迹的几种表示,简单多项式、B样条。
- 多项式
定义:通过多项式函数(如三次、五次、七次)显式表示轨迹,例如:

优点:
闭式解:可通过边界条件(位置、速度、加速度)直接求解系数,计算高效。
平滑性:高阶多项式可保证连续性
缺点:
全局性:调整任一系数会影响整个曲线,缺乏局部控制性。
数值不稳定:高阶多项式易出现震荡(Runge现象)。
典型应用:
无障碍物的点对点规划(如无人机最小加加速度轨迹)。
与庞特里亚金原理结合生成最优控制律。
- B样条
定义:由基函数(Basis Functions)和控制点线性组合生成的分段多项式曲线:

其中 为k阶B样条基函数,P_i为控制点。
为k阶B样条基函数,P_i为控制点。
优点:
局部性:修改单个控制点仅影响局部曲线(由基函数支撑区间决定)。
强凸包性:曲线始终位于控制点构成的凸包内。
灵活性:通过阶数k调节平滑性(如C^{k-2}连续)。
缺点:
非插值性:曲线通常不经过控制点(除非使用 clamped B-spline)。
参数复杂:需合理选择节点向量(knot vector)和控制点。
典型应用:
机器人运动规划(如避障路径的局部调整)。
CAD建模和动画轨迹生成。
**总结:**由于多项式显示表达轨迹,且比B样条计算简单,经常用于简单的无复杂约束的轨迹规划中;在有复杂约束的情况下(如避障等约束),多项式轨迹需要将梯度传导到多项式系数,而多项式系数没有物理意义,所以在优化过程中,可能梯度变化没有规律,不可直接解释,可能非常大然后又变得非常小;在B样条上就没有这样的问题,因为B样条是被控制点约束的,所以可以根据控制点的梯度直接调整控制点,这样物理意义明确,参数更好调,优化更加容易收敛;但是经过探索过后,发现可以经过一定的变化将多项式系数的梯度转换到路径点的梯度上,这就是Minco中提到的一部分工作,所以基于多项式的规划也可以将梯度链接到路径点了,而且由于多项式是显式经过路径点的(B样条不经过控制点),这一点上多项式轨迹更优。
那么多项式表达的轨迹难道真的更优吗,可能还不是,多项式轨迹具有全局性(牵一发动全身),而且还可能出现震荡的现象,就是说规划出的轨迹可能在某些情况下(边界状态变了一点、轨迹的某小段突然出现了个障碍物),轨迹会疯狂震荡,B样条由于具有局部性,数值稳定性比多项式好得多。这就是ego_planner v1和 v2的区别,v1用的是B样条,v2用的是minco处理后的多项式。经常有人说v2还不如v1,轨迹会打圈,可能就是上述的原因。
个人分析:B样条适合环境复杂约束下的轨迹规划,如避障等;多项式适合环境不复杂、计算速度有要求的轨迹规划,如无人机的高性能降落perching,跟踪、追击等。
2.2.1 均匀B样条
有关B样条的节点、阶数、控制点等可以看这个B样条曲线和Nurbs曲线 图文并茂的理解节点和节点区间。

这里s(t)是幂基函数,M是一个常量矩阵,q是控制点向量。

文中利用B样条的凸包性质保证轨迹的动态可行性(dynamic feasibility)及安全性(safety)。
动态可行性,文中构造的B样条的导数都是B样条,所以轨迹的速度加速度都在速度加速度样条控制点的凸包内如图3所示。安全性是使用了控制点到障碍物的距离和控制点之间的距离关系保证的:

由三角不等式得:

若满足 ,即满足
,即满足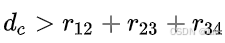 ,可得d_h>0。
,可得d_h>0。
2.2.2 优化问题构建
定义优化目标为:

式中,f_s f_c f_v f_a分别为平滑性、安全性、速度、加速度代价。
- 平滑代价
这里平滑代价也不是常见的jerk代价,因为后续的时间重分配会导致jerk代价变化,为了解耦这两部分,文中使用了基于轨迹形状的平滑性代价。使用了弹性带模型(Elastic Band):将轨迹视为由弹簧连接的节点(控制点),目标是最小化“弹簧力”的平方和。

当所有项为零时,控制点均匀分布在一条直线上(理想平滑轨迹)。

- 安全代价
这里意思就是让轨迹里障碍物的距离大于距离阈值d_{thr}。
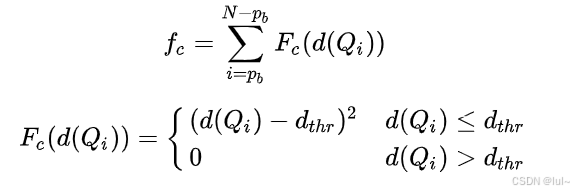
其中,d(Q_i)代表控制点距离障碍物的距离,是通过ESDF(Euclidean Signed Distance Functions/欧式符号距离场)地图查询得知的。
- 速度加速度代价

利用凸包性质限制轨迹的最大速度/加速度小于无人机的硬件最大速度/加速度。
2.2.3 优化问题求解
这里将碰撞约束、硬件约束构造到了目标函数中,使用了构造软约束的方法,其实其他的基于硬约束的方法然后使用增广拉格朗日函数法(ALM)也是类似的思想,只不过通过在最优达到后增大系数达到更硬的约束。
然后是基于梯度的优化求解(程序里是调用的nlopt库求解),先求出各个项对B样条控制点的梯度,再微调控制点让目标函数最小。
2.3 时间重分配
在后端轨迹优化过后,轨迹会远离障碍物,那么初始的分段轨迹每一段分配的飞行时间可能会有不合理的地方,相同的时间飞行更远的距离,虽然在优化过程中理论上会符合极值约束(实际也可能会超过),但是防止过度激进的动作,进行时间重分配是有必要的。

这个流程就是把不符合要求的速度加速度控制点根据放缩因子放缩来调整速度加速度而不改变轨迹的形状。
